Wéi fannen ech d'Gläichunge vun den Asymptoten vun der Hyperbola

Inhalt

Schrëtt
Method 1 vun 2: Factoring
Method 2 vun 2: Berechent Y
Tipps
Warnungen

Hyperbola Asymptoten sinn direkt Linnen, déi duerch den Zentrum vun der Hyperbola passéieren. D'Hyperbola kënnt op d'Asymptoten, awer iwwerquéiert se (oder beréiert se och ni). Et ginn zwou Weeër fir d'Gleichungen vun den Asymptoten ze fannen déi Iech hëllefen dat ganzt Konzept vun Asymptoten ze verstoen.

Schrëtt

Method 1 vun 2: Factoring

1 Schreift d'kanonesch Hyperbole Equatioun op. Loosst eis dat einfachst Beispill betruechten - en Hyperbola, deem säin Zentrum um Urspronk läit. An dësem Fall huet d'kanonesch Hyperbola Equatioun d'Form: /_a - /_b = 1 (wann d'Branchen vun der Hyperbola no riets oder no lénks geriicht sinn) oder /_b - /_a = 1 (wann d'Branchen vun der Hyperbola no uewen oder erof geriicht sinn). Denkt drun datt an dëser Equatioun, "x" an "y" Variabelen sinn, an "a" a "b" si Konstanten (dat heescht Zuelen).
- Beispill 1:/₉ - /₁₆ = 1
- E puer Enseignanten an Léierbuchautoren austauschen de konstante "a" a "b". Dofir studéiert d'Gleichung, déi Iech kritt gëtt fir ze verstoen wat wat ass. Memoréiert net nëmmen d'Gleichung - an dësem Fall wäert Dir näischt verstoen wann Variabelen an / oder Konstanten mat anere Symboler bezeechent ginn.
2 Setzt d'kanonesch Equatioun op Null (net een). Déi nei Equatioun beschreift béid Asymptoten, awer et brauch e puer Ustrengunge fir d'Gläichung fir all Asymptote ze kréien.
- Beispill 1:/₉ - /₁₆ = 0
3 Faktor déi nei Equatioun. Faktor déi lénks Säit vun der Gleichung. Denkt drun wéi eng quadratesch Equatioun ze faktoréieren, a liest weider.
- Déi lescht Gläichung (dat heescht d'faktoriséiert Equatioun) wäert (__ ± __) (__ ± __) = 0 sinn.
- Wann Dir déi éischt Begrëffer multiplizéiert (bannent all Paar Klammern), sollt Dir de Begrëff kréien /₉, also extrahéiert d'Quadratwuerzel vun dësem Member, a schreift d'Resultat amplaz vum éischte Raum an all Paar Klammern: (/₃ ± __)(/₃ ± __) = 0
- Ähnlech extrahéiert de Quadratwurzel vum Begrëff /₁₆, a schreift d'Resultat amplaz vum zweete Raum bannent all Paar Klammern: (//₃ ± /₄)(/₃ ± /₄) = 0
- Dir hutt all d'Konditioune vun der Gleichung fonnt, also bannent engem Paar Klameren tëscht de Begrëffer schreift e Pluszeechen, a bannent dem zweeten - e Minuszeechen, sou datt wann Dir multiplizéiert, déi entspriechend Begrëffer annuléiert ginn: (/₃ + /₄)(/₃ - /₄) = 0
4 Setzt all Binomial (dat heescht den Ausdrock bannent all Paar Klammern) op Null a berechent "y". Dëst wäert zwou Equatioune fannen, déi all Asymptote beschreiwen.
- Beispill 1: Wéi (/₃ + /₄)(/₃ - /₄) = 0, dann /₃ + /₄ = 0 an /₃ - /₄ = 0
- Schreift d'Gleichung wéi folgend: /₃ + /₄ = 0 → /₄ = - /₃ → y = - /₃
- Schreift d'Gleichung wéi folgend: /₃ - /₄ = 0 → - /₄ = - /₃ → y = /₃
5 Maacht déi beschriwwen Aktiounen mat engem Hyperbola deem seng Equatioun sech vun der kanonescher ënnerscheet. Am virege Schrëtt hutt Dir d'Gläichunge fir d'Asymptoten vun der Hyperbola fonnt, déi am Ursprong zentréiert sinn. Wann den Zentrum vun der Hyperbola op engem Punkt mat Koordinaten (h, k) ass, da gëtt et vun der folgender Equatioun beschriwwen: /_a - /_b = 1 oder /_b - /_a = 1. Dës Equatioun kann och faktoriséiert ginn. Awer an dësem Fall, beréiert net d'Binomien (x - h) an (y - k) bis Dir zum leschte Schrëtt kënnt.
- Beispill 2: /₄ - /₂₅ = 1
- Setzt dës Equatioun op 0 a faktoréiert se:
- (/₂ + /₅)(/₂ - /₅) = 0
- Gläicht all Binomial (dat heescht den Ausdrock bannent all Paar Klammern) op Null a berechent "y" fir d'Gleichungen fir d'Asymptoten ze fannen:
- /₂ + /₅ = 0 → y = - /₂x + /₂
- (/₂ - /₅) = 0 → y = /₂x - /₂

Method 2 vun 2: Berechent Y

1 Isoléiert den y Begrëff op der lénker Säit vun der Hyperbola Equatioun. Benotzt dës Method wann d'Hyperbola Equatioun a quadratescher Form ass. Och wann eng kanonesch Hyperbola Equatioun gëtt, erlaabt dës Method e bessert Verständnis vum Konzept vun Asymptoten. Isoléiert y oder (y - k) op der lénker Säit vun der Gleichung.
- Beispill 3:/₁₆ - /₄ = 1
- Füügt x op béid Säiten vun der Gleichung un, a multiplizéiert dann zwou Säiten mat 16:
- (y + 2) = 16 (1 + /₄)
- Vereinfach déi resultéierend Equatioun:
- (y + 2) = 16 + 4 (x + 3)
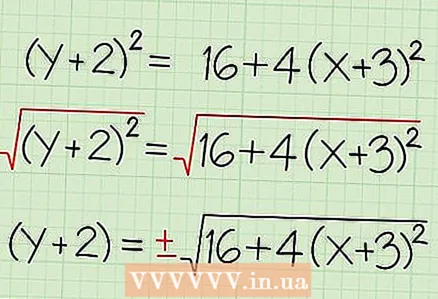2 Huelt de Quadratwurzel vun all Säit vun der Equatioun. Wéi och ëmmer, iwwersimplizéiert déi riets Säit vun der Gleichung net, well wann Dir de Quadratwurzel extrahéiert, kritt Dir zwee Resultater -positiv an negativ (zum Beispill -2 * -2 = 4, also √4 = 2 an √4 = -2). Fir béid Resultater ze lëschten, benotzt den ± Symbol.
- √ ((y + 2)) = √ (16 + 4 (x + 3))
- (y + 2) = ± √ (16 + 4 (x + 3))
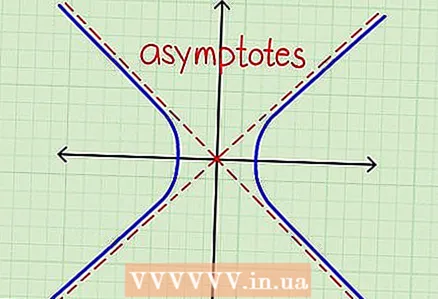3 Verstinn d'Konzept vun Asymptoten. Maacht dëst ier Dir op den nächste Schrëtt weidergeet. Eng Asymptote ass eng riicht Linn, op déi d'Hyperbola mat ëmmer méi Wäerter vun "x" kënnt.D'Hyperbola wäert d'Asymptote ni iwwerqueren, awer mat erhéijen "x" kënnt d'Hyperbola op den Asymptote op eng onendlech kleng Distanz.
4 Transforméiert d'Gläichung fir grouss x Wäerter ze berechnen. In der Regel, wann Dir mat de Gleichungen vun Asymptoten schafft, gi nëmme grouss Wäerter vun "x" berécksiichtegt (dat heescht déi Wäerter déi onendlech tendéieren). Dofir kënne verschidde Konstanten an der Equatioun vernoléissegt ginn, well hire Bäitrag kleng ass am Verglach mam "x". Zum Beispill, wann d'Variabel "x" mat e puer Milliarde gläich ass, da füügt d'Zuel (konstant) 3 e vernoléissegen Effekt op de Wäert vun "x".
- An der Equatioun (y + 2) = ± √ (16 + 4 (x + 3)) wéi "x" onendlech tendéiert, kann de konstante 16 vernoléissegt ginn.
- Fir grouss Wäerter vun "x" (y + 2) ≈ ± √ (4 (x + 3))
5 Berechent y fir d'Gläichunge fir d'Asymptoten ze fannen. Wann Dir vun de Konstante lassgitt, kënnt Dir de radikalen Ausdrock vereinfachen. Denkt drun datt Dir zwou Gleichungen an Ärer Äntwert musst schreiwen - eng mat engem Pluszeechen an déi aner mat engem Minuszeechen.
- y + 2 = ± √ (4 (x + 3) ^ 2)
- y + 2 = ± 2 (x + 3)
- y + 2 = 2x + 6 an y + 2 = -2x - 6
- y = 2x + 4any = -2x - 8

Tipps

Denkt drun datt d'Gleichung vun der Hyperbola an d'Gleichungen vun hiren Asymptoten ëmmer Konstanten (Konstanten) enthalen.
Eng equilateral Hyperbola ass eng Hyperbola an der Equatioun vun där a = b = c (konstant).
Wann eng equilateral Hyperbola Equatioun kritt gëtt, konvertéiert se als éischt a kanonesch Form a fënnt dann d'Gleichungen fir d'Asymptoten.