Wéi eng linear Diophantin Equatioun ze léisen

Auteur: Mark Sanchez
Denlaod Vun Der Kreatioun: 5 Januar 2021
Update Datum: 1 Juli 2024
Anonim
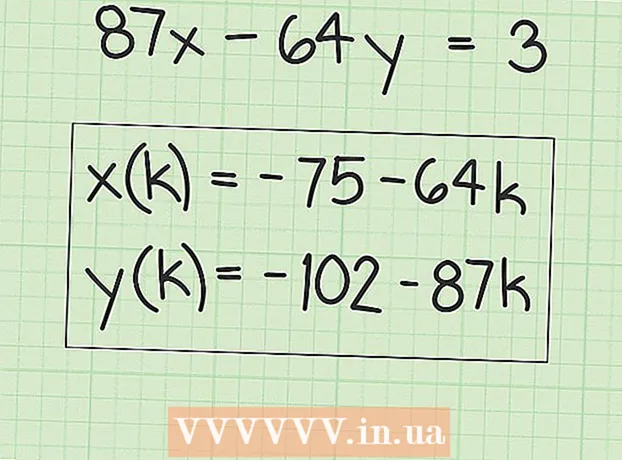
Wéi eng linear Diophantin Equatioun ze léisen - Gesellschaft
Wéi eng linear Diophantin Equatioun ze léisen - Gesellschaft

Inhalt

Fir eng linear Diophantin Equatioun ze léisen, musst Dir d'Wäerter vun de Variabelen "x" an "y" fannen, déi ganz Zuelen sinn. Eng ganz Zuel Léisung ass méi komplex wéi soss an erfuerdert e spezifesche Set vun Aktiounen. Als éischt musst Dir de gréisste gemeinsame Divisor (GCD) vun de Koeffizienten berechnen, an dann eng Léisung fannen. Wann Dir eng ganz Zuel Léisung fir eng linear Equatioun fonnt hutt, kënnt Dir en einfacht Muster benotze fir eng onendlech Unzuel vun anere Léisungen ze fannen.

Schrëtt

Deel 1 vu 4: Wéi eng Equatioun ze schreiwen

  1. 1 Schreift d'Gläichung a Standardform erof. Eng linear Equatioun ass eng Equatioun an där d'Exponente vun de Variabelen net méi héich sinn 1. Fir sou eng linear Equatioun ze léisen, schreift se als éischt a Standardform. D'Standardform vun enger linearer Equatioun gesäit esou aus: A.x+B.y=C{ displaystyle Axe + By = C}, wou A.,B.{ displaystyle A, B} an C{ displaystyle C} - ganz Zuelen.
    • Wann d'Gläichung an enger anerer Form gëtt, bréngt se op Standardform mat Basis algebraesche Operatiounen. Zum Beispill, no der Equatioun 23x+4y−7x=−3y+15{ Displaystyle 23x + 4y -7x = -3y + 15}... Gitt ähnlech Begrëffer a schreift d'Gleichung esou: 16x+7y=15{ Displaystyle 16x + 7y = 15}.
  2. 2 Vereinfach d'Gleichung (wa méiglech). Wann Dir d'Gläichung a Standardform schreift, kuckt op d'Koeffizienten A.,B.{ displaystyle A, B} an C{ displaystyle C}... Wann dës Chance e GCD hunn, deelt se all dräi Chance domat. D'Léisung fir sou eng vereinfacht Gleichung wäert och d'Léisung vun der ursprénglecher Equatioun sinn.
    • Zum Beispill, wann all dräi Koeffizienten gläich sinn, deelt se mat op d'mannst 2. Zum Beispill:
      • 42x+36y=48{ Displaystyle 42x + 36y = 48} (all Member ass deelbar mat 2)
      • 21x+18y=24{ Displaystyle 21x + 18y = 24} (elo sinn all Member deelbar mat 3)
      • 7x+6y=8{ displaystyle 7x + 6y = 8} (dës Equatioun kann net méi vereinfacht ginn)
  3. 3 Préift ob d'Gläichung geléist ka ginn. An e puer Fäll kënnt Dir direkt soen datt d'Gleichung keng Léisungen huet. Wann de Koeffizient "C" net deelbar ass vum GCD vun de Koeffizienten "A" a "B", huet d'Gleichung keng Léisungen.
    • Zum Beispill, wa béid Koeffizienten A.{ displaystyle A} an B.{ displaystyle B} si gläich, dann ass de Koeffizient C{ displaystyle C} muss gläich sinn. Awer wann C{ displaystyle C} komesch, da gëtt et keng Léisung.
      • Der Equatioun 2x+4y=21{ Displaystyle 2x + 4y = 21} keng ganz Zuel Léisungen.
      • Der Equatioun 5x+10y=17{ Displaystyle 5x + 10y = 17} et gi keng ganz Zuel Léisunge well déi lénks Säit vun der Equatioun deelt mat 5 an déi riets Säit net.

Deel 2 vu 4: Wéi schreift den Euclid Algorithmus

  1. 1 Verstinn den Euklids Algorithmus. Et ass eng Serie vu widderholl Divisiounen an deenen de virege Rescht als nächste Divisor benotzt gëtt. Dee leschte Divisor deen d'Zuelen integral deelt ass de gréisste gemeinsame Divisor (GCD) vun den zwou Zuelen.
    • Zum Beispill, loosst eis de GCD vun den Zuelen 272 a 36 mam Euclid Algorithmus fannen:
      • 272=7∗36+20{ Displaystyle 272 = 7 * 36 + 20} - Deelt déi gréisser Zuel (272) vun der klenger (36) a passt op de Rescht op (20);
      • 36=1∗20+16{ Displaystyle 36 = 1 * 20 + 16} - de fréiere Divisor (36) duerch de virege Rescht (20) deelen. Notéiert den neie Rescht (16);
      • 20=1∗16+4{ displaystyle 20 = 1 * 16 + 4} - de fréiere Divisor (20) duerch de virege Rescht (16) deelen. Notéiert den neie Rescht (4);
      • 16=4∗4+0{ Displaystyle 16 = 4 * 4 + 0} - Deelt de viregte Divisor (16) mam fréiere Rescht (4). Well de Rescht 0 ass, kënne mir soen datt 4 de GCD vun den originellen zwou Zuelen 272 a 36 ass.
  2. 2 Benotzt den Euclid Algorithmus fir d'Koeffizienten "A" a "B". Wann Dir déi linear Equatioun a Standardform schreift, bestëmmt d'Koeffizienten "A" a "B" an setzt dann den Euclid Algorithmus op hinnen fir de GCD ze fannen. Zum Beispill, gitt eng linear Equatioun 87x−64y=3{ Displaystyle 87x-64y = 3}.
    • Hei ass den Euclid Algorithmus fir Koeffizienten A = 87 a B = 64:
      • 87=1∗64+23{ displaystyle 87 = 1 * 64 + 23}
      • 64=2∗23+18{ displaystyle 64 = 2 * 23 + 18}
      • 23=1∗18+5{ displaystyle 23 = 1 * 18 + 5}
      • 18=3∗5+3{ displaystyle 18 = 3 * 5 + 3}
      • 5=1∗3+2{ displaystyle 5 = 1 * 3 + 2}
      • 3=1∗2+1{ Displaystyle 3 = 1 * 2 + 1}
      • 2=2∗1+0{ displaystyle 2 = 2 * 1 + 0}
  3. 3 Fannt de Gréisste Common Factor (GCD). Zënter datt de leschte Divisor 1 war, sinn GCD 87 a 64 1. Also, 87 a 64 si Primzuelen relativ zueneen.
  4. 4 Analyséiert d'Resultat. Wann Dir d'Gcd Koeffizienten fannt A.{ displaystyle A} an B.{ displaystyle B}, vergläicht et mam Koeffizient C{ displaystyle C} d'Original Equatioun. Wann C{ displaystyle C} deelbar mat gcd A.{ displaystyle A} an B.{ displaystyle B}, der Equatioun huet eng ganz Zuel Léisung; soss huet d'Gleichung keng Léisungen.
    • Zum Beispill d'Gläichung 87x−64y=3{ Displaystyle 87x-64y = 3} kann geléist ginn well 3 deelbar ass mat 1 (gcd = 1).
    • Zum Beispill, unhuelen GCD = 5. 3 ass net gläichméisseg deelbar mat 5, sou datt dës Equatioun keng ganz Zuel Léisungen huet.
    • Wéi hei ënnendrënner gewisen, wann eng Equatioun eng ganz Zuel Léisung huet, huet se och eng onendlech Unzuel vun anere ganzer Léisungen.

Deel 3 vu 4: Wéi fannt Dir eng Léisung mam Euklids Algorithmus

  1. 1 Nummer d'Schrëtt fir d'GCD ze berechnen. Fir d'Léisung fir eng linear Equatioun ze fannen, musst Dir den Euklidesche Algorithmus als Basis fir den Ersatz- a Vereinfachungsprozess benotzen.
    • Start mat der Nummeréierung vun de Schrëtt fir d'Berechnung vum GCD. De Berechnungsprozess gesäit esou aus:
      • Schrëtt 1:87=(1∗64)+23{ Displaystyle { text {Schrëtt 1}}: 87 = (1 * 64) +23}
      • Schrëtt 2:64=(2∗23)+18{ Displaystyle { text {Schrëtt 2}}: 64 = (2 * 23) +18}
      • Schrëtt 3:23=(1∗18)+5{ Displaystyle { text {Schrëtt 3}}: 23 = (1 * 18) +5}
      • Schrëtt 4:18=(3∗5)+3{ Displaystyle { text {Schrëtt 4}}: 18 = (3 * 5) +3}
      • Schrëtt 5:5=(1∗3)+2{ Displaystyle { text {Schrëtt 5}}: 5 = (1 * 3) +2}
      • Schrëtt 6:3=(1∗2)+1{ Displaystyle { text {Schrëtt 6}}: 3 = (1 * 2) +1}
      • Schrëtt 7:2=(2∗1)+0{ Displaystyle { text {Schrëtt 7}}: 2 = (2 * 1) +0}
  2. 2 Passt op de leschte Schrëtt op, wou et e Rescht ass. Schreift d'Gleichung fir dëse Schrëtt fir de Rescht ze isoléieren.
    • An eisem Beispill ass de leschte Schrëtt mam Rescht Schrëtt 6. De Rescht ass 1. Schreift d'Gleichung am Schrëtt 6 wéi folgend:
      • 1=3−(1∗2){ Displaystyle 1 = 3- (1 * 2)}
  3. 3 Isoléiert de Rescht vum virege Schrëtt. Dëse Prozess ass e Schrëtt-fir-Schrëtt "no uewen". All Kéier wäert Dir de Rescht an der Equatioun am virege Schrëtt isoléieren.
    • Isoléiert de Rescht vun der Equatioun am Schrëtt 5:
      • 2=5−(1∗3){ displaystyle 2 = 5- (1 * 3)} oder 2=5−3{ displaystyle 2 = 5-3}
  4. 4 Ersetzen a vereinfachen. Notéiert datt d'Gläichung am Schrëtt 6 d'Zuel 2 enthält, an an der Gläichung am Schrëtt 5 ass d'Zuel 2 isoléiert. Also amplaz vun "2" an der Equatioun am Schrëtt 6, ersetzt den Ausdrock am Schrëtt 5:
    • 1=3−2{ Displaystyle 1 = 3-2} (Equatioun vu Schrëtt 6)
    • 1=3−(5−3){ displaystyle 1 = 3- (5-3)} (amplaz vun 2 gouf en Ausdrock ersat)
    • 1=3−5+3{ displaystyle 1 = 3-5 + 3} (Klammeren opgemaach)
    • 1=2(3)−5{ Displaystyle 1 = 2 (3) -5} (vereinfacht)
  5. 5 Widderhuelen de Substitutiouns- a Vereinfachungsprozess. Widderhuelen de beschriwwene Prozess, plënnert duerch den Euklidesche Algorithmus an ëmgedréinter Uerdnung. All Kéier wäert Dir d'Gläichung vum virege Schrëtt nei schreiwen an et an déi lescht Equatioun pluggen déi Dir kritt.
    • De leschte Schrëtt, op dee mir gekuckt hunn, war Schrëtt 5. Also gitt op Schrëtt 4 an isoléiert de Rescht an der Equatioun fir dee Schrëtt:
      • 3=18−(3∗5){ Displaystyle 3 = 18- (3 * 5)}
    • Ersetzt dësen Ausdrock fir "3" an der leschter Equatioun:
      • 1=2(18−3∗5)−5{ Displaystyle 1 = 2 (18-3 * 5) -5}
      • 1=2(18)−6(5)−5{ Displaystyle 1 = 2 (18) -6 (5) -5}
      • 1=2(18)−7(5){ Displaystyle 1 = 2 (18) -7 (5)}
  6. 6 Fuert weider mam Ersatz- a Vereinfachungsprozess. Dëse Prozess gëtt widderholl bis Dir den initialen Schrëtt vum Euklidesche Algorithmus erreecht. D'Zil vum Prozess ass d'Gläichung mat de Koeffizienten 87 an 64 vun der ursprénglecher Equatioun ze schreiwen fir ze léisen. An eisem Beispill:
    • 1=2(18)−7(5){ Displaystyle 1 = 2 (18) -7 (5)}
    • 1=2(18)−7(23−18){ displaystyle 1 = 2 (18) -7 (23-18)} (den Ausdrock vum Schrëtt 3 ersat)
      • 1=2(18)−7(23)+7(18){ displaystyle 1 = 2 (18) -7 (23) +7 (18)}
      • 1=9(18)−7(23){ Displaystyle 1 = 9 (18) -7 (23)}
    • 1=9(64−2∗23)−7(23){ Displaystyle 1 = 9 (64-2 * 23) -7 (23)} (den Ausdrock vum Schrëtt 2 ersat)
      • 1=9(64)−18(23)−7(23){ displaystyle 1 = 9 (64) -18 (23) -7 (23)}
      • 1=9(64)−25(23){ displaystyle 1 = 9 (64) -25 (23)}
    • 1=9(64)−25(87−64){ displaystyle 1 = 9 (64) -25 (87-64)} (den Ausdrock vum Schrëtt 1 ersat)
      • 1=9(64)−25(87)+25(64){ displaystyle 1 = 9 (64) -25 (87) +25 (64)}
      • 1=34(64)−25(87){ Displaystyle 1 = 34 (64) -25 (87)}
  7. 7 Schreift déi resultéierend Gläichung no den originelle Koeffizienten of. Wann Dir op den éischte Schrëtt vum Euklidesche Algorithmus zréckkommt, gesitt Dir datt déi resultéierend Equatioun zwee Koeffizienten vun der ursprénglecher Equatioun enthält. Schreift d'Gleichung sou datt d'Uerdnung vu senge Begrëffer mat de Koeffizienten vun der ursprénglecher Equatioun passt.
    • An eisem Beispill, d'Original Equatioun 87x−64y=3{ Displaystyle 87x-64y = 3}... Dofir, iwwerschreift déi resultéierend Equatioun sou datt d'Koeffizienten an d'Linn bruecht ginn.Bezuelt besonnesch Opmierksamkeet fir de Koeffizient "64". An der ursprénglecher Equatioun ass dëse Koeffizient negativ, an am Euklidesche Algorithmus ass hien positiv. Dofir muss de Faktor 34 negativ gemaach ginn. Déi lescht Equatioun gëtt esou geschriwwen:
      • 87(−25)−64(−34)=1{ displaystyle 87 (-25) -64 (-34) = 1}
  8. 8 Benotzt de passenden Multiplikator fir eng Léisung ze fannen. Notéiert datt an eisem Beispill, GCD = 1, also ass déi lescht Gläichung 1. Awer d'Original Equatioun (87x-64y) ass 3. Dofir mussen all Begrëffer an der Finale Equatioun mat 3 multiplizéiert ginn fir d'Léisung ze kréien:
    • 87(−25∗3)−64(−34∗3)=1∗3{ Displaystyle 87 (-25 * 3) -64 (-34 * 3) = 1 * 3}
    • 87(−75)−64(−102)=3{ displaystyle 87 (-75) -64 (-102) = 3}
  9. 9 Schreift d'Integer Léisung fir d'Gleichung op. D'Zuelen, déi mat de Koeffizienten vun der ursprénglecher Equatioun multiplizéiert ginn, sinn d'Léisunge fir dës Equatioun.
    • An eisem Beispill schreift d'Léisung als e Paar Koordinaten: (x,y)=(−75,−102){ displaystyle (x, y) = ( - 75, -102)}.

Deel 4 vu 4: Fannt Onendlech Aner Léisungen

  1. 1 Verstitt datt et eng onendlech Unzuel u Léisunge gëtt. Wann eng linear Equatioun eng ganz Zuel Léisung huet, da muss se onendlech vill ganz Léisungen hunn. Hei ass e séieren Beweis (an algebraescher Form):
    • A.x+B.y=C{ displaystyle Axe + By = C}
    • A.(x+B.)+B.(y−A.)=C{ Display A (x + B) + B (y-A) = C} (wann Dir "B" op "x" addéiert an "A" vun "y" subtrahéiert, ännert de Wäert vun der ursprénglecher Equatioun net)
  2. 2 Notéiert déi originell x an y Wäerter. D'Schabloun fir déi nächst (onendlech) Léisungen ze berechnen fänkt mat der eenzeger Léisung un déi Dir scho fonnt hutt.
    • An eisem Beispill ass d'Léisung e Paar Koordinaten (x,y)=(−75,−102){ displaystyle (x, y) = ( - 75, -102)}.
  3. 3 Fügt den "B" Faktor zum "x" Wäert derbäi. Maacht dëst fir den neien x Wäert ze fannen.
    • An eisem Beispill, x = -75, a B = -64:
      • x=−75+(−64)=−139{ displaystyle x = -75 + ( - 64) = - 139}
    • Also, den neie Wäert "x": x = -139.
  4. 4 Subtract den "A" Faktor vum "y" Wäert. Also datt de Wäert vun der ursprénglecher Equatioun net ännert, wann Dir eng Nummer op "x" derbäigesat, musst Dir eng aner Nummer vun "y" subtrahéieren.
    • An eisem Beispill, y = -102, an A = 87:
      • y=−102−87=−189{ Displaystyle y = -102-87 = -189}
    • Also, den neie Wäert fir "y": y = -189.
    • Dat neit Koordinatpaar gëtt esou geschriwwen: (x,y)=(−139,−189){ displaystyle (x, y) = ( - 139, -189)}.
  5. 5 Préift d'Léisung. Fir z'iwwerpréiwen ob dat neit Koordinatpaar eng Léisung fir déi originell Equatioun ass, pluggelt d'Wäerter an d'Gleichung.
    • 87x−64y=3{ Displaystyle 87x-64y = 3}
    • 87(−139)−64(−189)=3{ displaystyle 87 (-139) -64 (-189) = 3}
    • 3=3{ displaystyle 3 = 3}
    • Well d'Gläichheet erfëllt ass, ass d'Entscheedung richteg.
  6. 6 Schreift Ausdréck fir vill Léisungen ze fannen. D '"x" Wäerter si gläich mat der ursprénglecher Léisung plus all Multiple vum "B" Faktor. Dëst kann als folgenden Ausdrock geschriwwe ginn:
    • x (k) = x + k (B), wou "x (k)" de Set vu "x" Wäerter ass an "x" den originelle (éischte) Wäert vun "x" ass deen Dir fonnt hutt.
      • An eisem Beispill:
      • x(k)=−75−64k{ Displaystyle x (k) = - 75-64k}
    • y (k) = y-k (A), wou y (k) de Set vun y Wäerter ass an y den originalen (éischte) y Wäert ass deen Dir fonnt hutt.
      • An eisem Beispill:
      • y(k)=−102−87k{ Displaystyle y (k) = - 102-87k}

Mir Recommandéieren

Wéi maache ech Screenshots mat OneNote
Wéi maache ech Screenshots mat OneNote
Wéi läschen ech e Filter an Excel
Wéi läschen ech e Filter an Excel
Wéi mat Oflehnung ëmgoen
Wéi mat Oflehnung ëmgoen
Wéi vermeit Dir Äre Computer mat engem Virus oder Wuerm ze infizéieren
Wéi vermeit Dir Äre Computer mat engem Virus oder Wuerm ze infizéieren