Wéi een Matricen deelt

Inhalt

Kuerze Resumé
Schrëtt
Deel 1 vun 3: Testen vun der Divisibilitéit vu Matricen
Deel 2 vun 3: Fannt d'Inverse Matrix
Deel 3 vun 3: Matrixmultiplikatioun
Tipps
Warnungen
Zousätzlech Artikelen

Wann Dir wësst wéi Dir zwee Matrixen multiplizéiert, kënnt Dir ufänken d'Matricen ze "deelen". D'Wuert "Divisioun" ass an Zitatzeechen zougemaach, well Matrixen tatsächlech net kënnen opgedeelt ginn. D'Divisiounsoperatioun gëtt ersat duerch d'Operatioun vun enger Matrix mat enger Matrix ze multiplizéieren déi invers vun der zweeter Matrix ass. Fir Einfachheet, betruecht e Beispill mat ganz Zuelen: 10 ÷ 5. Fannt de Géigesaz vu 5: 5 oder /₅, an ersetzt dann d'Divisioun duerch Multiplikatioun: 10 x 5; d'Resultat vun der Divisioun an der Multiplikatioun wäert d'selwecht sinn. Dofir gëtt ugeholl datt d'Divisioun duerch d'Multiplikatioun duerch déi invers Matrix ersat ka ginn. Typesch gi sou Berechnunge benotzt fir Systemer vu linearem Equatiounen ze léisen.

Kuerze Resumé

Dir kënnt Matricen net deelen. Amplaz ze deelen, gëtt eng Matrix multiplizéiert mam Inverse vun der zweeter Matrix. "Divisioun" vun zwou Matrixen [A] ÷ [B] ass wéi folgend geschriwwen: [A] * [B] oder [B] * [A].
Wann d'Matrix [B] net quadratesch ass, oder wann hiren Determinant 0 ass, schreift "keng eendeiteg Léisung." Soss, fannt den Determinant vun der Matrix [B] a gitt op den nächste Schrëtt.
Fannt den Inverse: [B].
Multiplizéieren Matrixen fir [A] * [B] oder [B] * [A] ze fannen. Denkt drun datt d'Uerdnung an där d'Matriken multiplizéiert sinn um Ennresultat beaflosst (dat heescht d'Resultater kënne variéieren).

Schrëtt

Deel 1 vun 3: Testen vun der Divisibilitéit vu Matricen

1 Verstinn d '"Divisioun" vu Matricen. Tatsächlech kënnen d'Matriken net opgedeelt ginn. Et gëtt keng sou mathematesch Operatioun wéi "eng Matrix vun enger anerer deelen". Divisioun gëtt ersat andeems eng Matrix multiplizéiert gëtt mat der Invers vun der zweeter Matrix. Dat ass, d'Notatioun [A] ÷ [B] ass net richteg, sou datt se duerch déi folgend Notatioun ersat gëtt: [A] * [B]. Well béid Entréen gläichwäerteg sinn am Fall vu Skalar Wäerter, kënne mir theoretesch iwwer "Divisioun" vu Matrix schwätzen, awer et ass ëmmer besser déi richteg Terminologie ze benotzen.
- Notéiert datt [A] * [B] an [B] * [A] verschidden Operatiounen sinn. Et kann néideg sinn fir béid Operatiounen auszeféieren fir all méiglech Léisungen ze fannen.
- Zum Beispill, amplaz ${ displaystyle { begin {pmatrix} 13 & 26 39 & 13 end {pmatrix}} div { begin {pmatrix} 7 & 4 2 & 3 end {pmatrix}}}}$ aschreiwen ${ displaystyle { begin {pmatrix} 13 & 26 39 & 13 end {pmatrix}} * { begin {pmatrix} 7 & 4 2 & 3 end {pmatrix}} ^ {- 1} }$ .
  Dir musst vläicht berechnen ${ displaystyle { begin {pmatrix} 7 & 4 2 & 3 end {pmatrix}} ^ {- 1} * { begin {pmatrix} 13 & 26 39 & 13 end {pmatrix}} }$ fir en anert Resultat ze kréien.
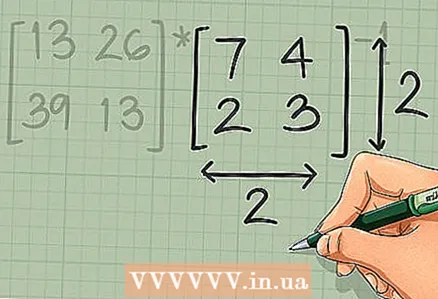2 Gitt sécher datt d'Matrix mat där Dir déi aner Matrix "deelt" ass quadratesch. Fir eng Matrix ëmzegoen (fënnt den Invers vun enger Matrix), muss se quadratesch sinn, dat heescht mat der selwechter Unzuel vu Reien a Kolonnen. Wann d'invertéiert Matrix net invers ass, gëtt et keng definitiv Léisung.
- Erëm, d'Matriken sinn hei net "deelbar". An der Operatioun [A] * [B] bezitt déi beschriwwen Bedingung sech op d'Matrix [B]. An eisem Beispill bezitt dës Bedingung op d'Matrix ${ displaystyle { begin {pmatrix} 7 & 4 2 & 3 end {pmatrix}}}$
- Eng Matrix déi ëmgedréit ka ginn heescht net degeneréiert oder reegelméisseg. Eng Matrix déi net ëmgedréint ka ginn, gëtt degeneréiert oder singular genannt.
3 Préift ob déi zwou Matricen multiplizéiert kënne ginn. Fir zwou Matricen ze multiplizéieren, muss d'Zuel vun de Sailen an der éischter Matrix gläich sinn mat d'Zuel vun de Reien an der zweeter Matrix. Wann dës Bedingung net an der Entrée [A] * [B] oder [B] * [A] erfëllt ass, gëtt et keng Léisung.
- Zum Beispill, wann d'Gréisst vun der Matrix [A] 4 x 3 ass an d'Gréisst vun der Matrix [B] 2 x 2 ass, gëtt et keng Léisung. Dir kënnt [A] * [B] net multiplizéieren well 4 ≠ 2, an Dir kënnt net [B] * [A] multiplizéieren well 2 ≠ 3.
- Notéiert datt d'invers Matrix [B] ëmmer déiselwecht Unzuel vu Reien a Kolonnen huet wéi déi originell Matrix [B]. Et ass net néideg déi invers Matrix ze fannen fir z'iwwerpréiwen ob zwou Matricen multiplizéiert kënne ginn.
- An eisem Beispill ass d'Gréisst vu béide Matricen 2 x 2, sou datt se an all Uerdnung multiplizéiert kënne ginn.
4 Fannt den Determinant vun der 2 × 2 Matrix. Denkt drun: Dir kënnt eng Matrix nëmmen ëmdréinen wann hiren Determinant net null ass (soss kënnt Dir d'Matrix net ëmgoen). Hei ass wéi Dir den Determinant vun enger 2 x 2 Matrix fannt:
- 2 x 2 Matrix: Determinant vun enger Matrix ${ displaystyle { begin {pmatrix} a & b c & d end {pmatrix}}}$ ass gläich wéi ad - bc. Dat heescht, vum Produkt vun den Elementer vun der Haaptdiagonal (passéiert duerch déi iewescht lénks a riets ënnescht riets Eck), subtrahéiere d'Produkter vun den Elementer vun der anerer Diagonal (passéiert duerch déi iewescht riets an déi ënnescht lénks Ecke).
- Zum Beispill den Determinant vun der Matrix ${ displaystyle { begin {pmatrix} 7 & 4 2 & 3 end {pmatrix}}}$ ass gläich wéi (7) (3) - (4) (2) = 21 - 8 = 13. Den Determinant ass nonzero, sou datt dës Matrix ëmgedréint ka ginn.
5 Fannt den Determinant vun der méi grousser Matrix. Wann d'Gréisst vun der Matrix 3 x 3 oder méi ass, ass den Determinant liicht méi schwéier ze berechnen.
- 3 x 3 Matrix: wielt all Element a kräizt d'Rei an d'Kolonn an där et ass.Fannt den Determinant vun der resultéierender 2 × 2 Matrix, a multiplizéiert se dann mam ausgewielten Element; spezifizéiert d'Zeeche vum Determinant an engem speziellen Dësch. Widderhuelen dëse Prozess fir déi aner zwee Elementer déi an der selwechter Zeil oder Kolonn sinn wéi den Artikel deen Dir gewielt hutt. Fannt dann d'Zomm vun den (dräi) Determinanten kritt. Liest dësen Artikel fir méi Informatioun iwwer wéi Dir den Determinant vun enger 3 x 3 Matrix fannt.
- Grouss Matrixen: den Determinant vun esou Matricen ass am beschte gesicht mat engem Grafikrechner oder Software. D'Method ass ähnlech wéi d'Method fir den Determinant vun enger 3 × 3 Matrix ze fannen, awer et ass zimmlech langweileg fir se manuell anzesetzen. Zum Beispill, fir den Determinant vun enger 4 x 4 Matrix ze fannen, musst Dir d'Determinante vu véier 3 x 3 Matricen fannen.
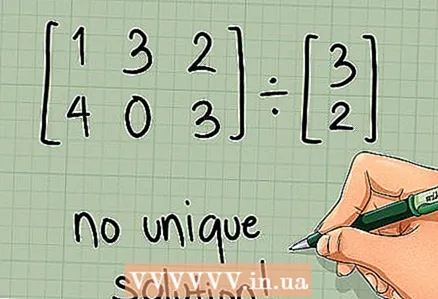6 Berechnunge weiderféieren. Wann d'Matrix net quadratesch ass oder wann hiren Determinant gläich mat Null ass, schreift "keng eendeiteg Léisung", dat heescht de Berechnungsprozess ass ofgeschloss. Wann d'Matrix quadratesch ass an en Net -Null Determinant huet, spréngt op déi nächst Sektioun.

Deel 2 vun 3: Fannt d'Inverse Matrix

1 Tauscht d'Elementer vun der Haaptdiagonal vun der 2 x 2 Matrix. Gitt eng 2 × 2 Matrix, benotzt déi séier invers Method. Éischt, tauscht dat uewe lénks Element an dat ënnen riets Element. Zum Beispill:
- ${ displaystyle { begin {pmatrix} 7 & 4 2 & 3 end {pmatrix}}}$ → ${ displaystyle { begin {pmatrix} 3 & 4 2 & 7 end {pmatrix}}}$
- Note: déi meescht Leit benotzen Rechner fir eng 3 x 3 (oder méi grouss) Matrix ëmzegoen. Wann Dir dëst manuell maache musst, gitt op d'Enn vun dëser Sektioun.
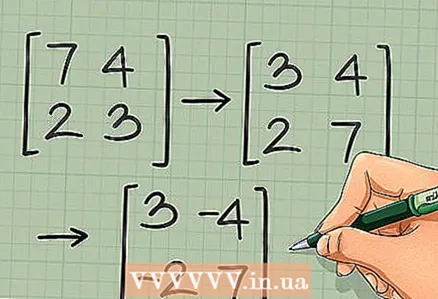2 Wielt déi reschtlech zwee Elementer net ëm, mee ännert hiren Zeechen. Dat ass, multiplizéiert dat uewe riets Element an dat ënnescht lénks Element mat -1:
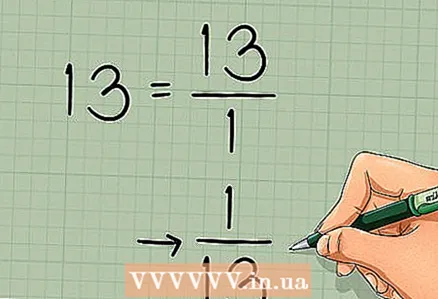- ${ displaystyle { begin {pmatrix} 3 & 4 2 & 7 end {pmatrix}}}$ → ${ displaystyle { begin {pmatrix} 3 & -4 - 2 & 7 end {pmatrix}}}$
3 Fannt de Géigesaz vum Determinant. Den Determinant vun dëser Matrix gouf an der viregter Sektioun fonnt, sou datt mir et net erëm berechnen. Den Invers vum Determinant gëtt wéi follegt geschriwwen: 1 / (Determinant):
- An eisem Beispill ass den Determinant 13. Reverse Wäert: ${ displaystyle { frac {1} {13}}}$ .
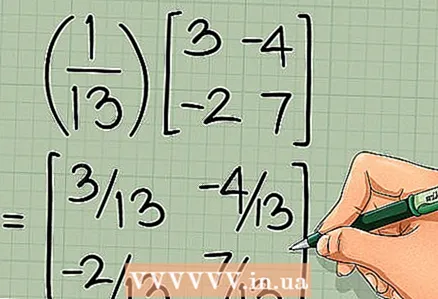4 Multiplikéiert déi resultéierend Matrix mat der Géigesäitegkeet vum Determinant. Multiplikéiert all Element vun der neier Matrix mam Inverse vum Determinant. Déi lescht Matrix ass den Invers vun der ursprénglecher 2 x 2 Matrix:
- ${ displaystyle { frac {1} {13}} * { begin {pmatrix} 3 & -4 - 2 & 7 end {pmatrix}}}$
  = ${ displaystyle { begin {pmatrix} { frac {3} {13}} & { frac {-4} {13}} { frac {-2} {13}} & { frac {7 } {13}} end {pmatrix}}}$
5 Kuckt ob d'Berechnungen richteg sinn. Fir dëst ze maachen, multiplizéiert d'Original Matrix mat hirer Invers. Wann d'Berechnunge richteg sinn, gëtt d'Produkt vun der ursprénglecher Matrix mam Inverse d'Identitéit Matrix: (1001){ displaystyle { begin {pmatrix} 1 & 0 0 & 1 end {pmatrix}}}... Wann den Test erfollegräich war, gitt op déi nächst Sektioun.
- An eisem Beispill: ${ displaystyle { begin {pmatrix} { frac {3} {13}} & { frac {-4} {13}} { frac {-2} {13}} & { frac {7 } {13}} end {pmatrix}} * { begin {pmatrix} 7 & 4 2 & 3 end {pmatrix}} = { begin {pmatrix} 1 & 0 0 & 1 end {pmatrix}}}$ .
- Fir méi Informatioun iwwer d'Matriken ze multiplizéieren, liest dësen Artikel.
- Notiz: d'Operatioun vun der Matrixmultiplikatioun ass net commutativ, dat heescht, d'Uerdnung vun de Matricen ass wichteg. Awer wann déi originell Matrix mat senger Invers multiplizéiert gëtt, féiert all Uerdnung zur Identitéitsmatrix.
6 Fannt d'Invers vun enger 3 x 3 Matrix (oder méi grouss). Wann Dir dëse Prozess scho kennt, ass et besser e Grafikrechner oder speziell Software ze benotzen. Wann Dir déi invers Matrix manuell muss fannen, gëtt de Prozess kuerz hei ënnen beschriwwen:
- Maacht mat der Identitéitsmatrix I op der rietser Säit vun der ursprénglecher Matrix. Zum Beispill, [B] → [B | Ech]. Fir d'Identitéit Matrix sinn all Elementer vun der Haaptdiagonal gläich wéi 1, an all aner Elementer si gläich wéi 0.
- Vereinfach d'Matrix sou datt seng lénks Säit getrëppelt gëtt; weider vereinfachen sou datt déi lénks Säit d'Identitéit Matrix gëtt.
- No der Vereinfachung hëlt d'Matrix déi folgend Form un: [I | B] an. Dat ass, seng riets Säit ass den Invers vun der ursprénglecher Matrix.

Deel 3 vun 3: Matrixmultiplikatioun

1 Schreift zwee méiglech Ausdréck op. D'Operatioun fir zwou Skalaren ze multiplizéieren ass kommutativ, dat heescht 2 x 6 = 6 x 2.Dëst ass net de Fall am Fall vun der Matrixmultiplikatioun, also musst Dir zwee Ausdréck léisen:
- x = [A] * [B] ass d'Léisung fir d'Gleichung x[B] = [A].
- x = [B] * [A] ass d'Léisung fir d'Gleichung [B]x = [A] dir.
- Féiert all mathematesch Operatioun op béide Säiten vun der Equatioun aus. Wann [A] = [C] dann [B] [A] ≠ [C] [B] well [B] lénks vun [A] awer riets vun [C] ass.
2 Bestëmmt d'Gréisst vun der leschter Matrix. D'Gréisst vun der leschter Matrix hänkt vun der Gréisst vun de multiplizéierte Matrix of. D'Zuel vun de Reien an der leschter Matrix ass d'selwecht wéi d'Zuel vun de Reien an der éischter Matrix, an d'Zuel vun de Säulen an der leschter Matrix ass d'selwecht wéi d'Zuel vun de Sailen an der zweeter Matrix.
- An eisem Beispill d'Gréisst vu béide Matricen ${ displaystyle { begin {pmatrix} 13 & 26 39 & 13 end {pmatrix}}}$ an ${ displaystyle { begin {pmatrix} { frac {3} {13}} & { frac {-4} {13}} { frac {-2} {13}} & { frac {7 } {13}} end {pmatrix}}}$ ass 2 x 2, sou datt d'Gréisst vun der ursprénglecher Matrix 2 x 2 ass.
- Betruecht e méi komplex Beispill: wann d'Gréisst vun der Matrix [A] ass 4 x 3, an d'Gréisst vun der Matrix [B] ass 3 x 3, dann ass déi lescht Matrix [A] * [B] 4 x 3.
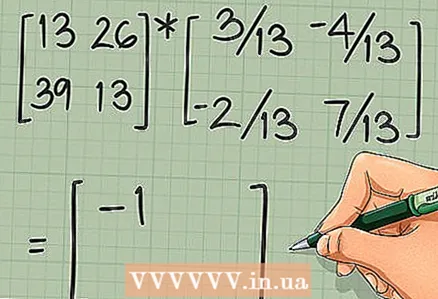3 Fannt de Wäert vum éischte Element. Liest dësen Artikel oder erënnert Iech un déi folgend Basis Schrëtt:
- Fir dat éischt Element (éischt Zeil, éischt Kolonn) vun der leschter Matrix [A] [B] ze fannen, berechent de Punktprodukt vun den Elementer vun der éischter Zeil vun der Matrix [A] an d'Elementer vun der éischter Kolonn vun der Matrix [B ]. Am Fall vun enger 2 x 2 Matrix gëtt de Punktprodukt wéi follegt berechent: ${ displaystyle a_ {1,1} * b_ {1,1} + a_ {1,2} * b_ {2,1}}$ .
- An eisem Beispill: ${ displaystyle { begin {pmatrix} 13 & 26 39 & 13 end {pmatrix}} * { begin {pmatrix} { frac {3} {13}} & { frac {-4} { 13}} { frac {-2} {13}} & { frac {7} {13}} end {pmatrix}}}$ ... Also ass dat éischt Element vun der leschter Matrix d'Element:
  ${ displaystyle (13 * { frac {3} {13}}) + (26 * { frac {-2} {13}})}}$
  ${ displaystyle = 3 + -4}$
  ${ displaystyle = -1}$
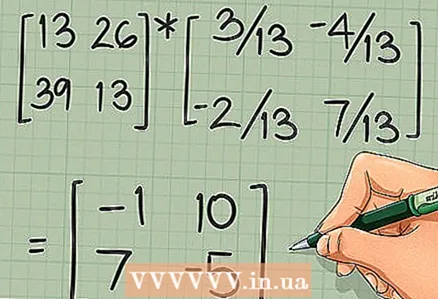4 Fuert weider mat Punktprodukter ze berechnen fir all Element vun der leschter Matrix ze fannen. Zum Beispill ass d'Element an der zweeter Zeil an der éischter Kolonn gläich mam Punktprodukt vun der zweeter Zeil vun der Matrix [A] an der éischter Kolonn vun der Matrix [B]. Probéiert déi verbleiwen Elementer selwer ze fannen. Dir sollt déi folgend Resultater kréien:
- ${ displaystyle { begin {pmatrix} 13 & 26 39 & 13 end {pmatrix}} * { begin {pmatrix} { frac {3} {13}} & { frac {-4} { 13}} { frac {-2} {13}} & { frac {7} {13}} end {pmatrix}} = { begin {pmatrix} -1 & 10 7 & -5 Enn {pmatrix}}}$
- Wann Dir eng aner Léisung braucht ze fannen: ${ displaystyle { begin {pmatrix} { frac {3} {13}} & { frac {-4} {13}} { frac {-2} {13}} & { frac {7 } {13}} end {pmatrix}} * { begin {pmatrix} 13 & 26 39 & 13 end {pmatrix}} = { begin {pmatrix} -9 & 2 19 & 3 Enn {pmatrix}}}$

Tipps

D'Matrix kann an eng Skalar opgedeelt ginn; dofir gëtt all Element vun der Matrix duerch eng Skalar gedeelt.
- Zum Beispill, wann d'Matrix ${ displaystyle { begin {pmatrix} 6 & 8 2 & 4 end {pmatrix}}}$ gedeelt duerch 2, kritt Dir d'Matrix ${ displaystyle { begin {pmatrix} 3 & 4 1 & 2 end {pmatrix}}}$

Warnungen

De Rechner gëtt net ëmmer absolut korrekt Resultater wann et ëm Matrixberechnunge geet. Zum Beispill, wann de Rechner behaapt datt den Artikel eng ganz kleng Zuel ass (wéi 2E), ass de Wäert héchstwahrscheinlech null.