Inhalt

• Schrëtt
• Method 1 vun 3: Wéi eng kubesch Equatioun ouni konstante Begrëff ze léisen
• Method 2 vun 3: Wéi fannt Dir ganz Roots Mat Multiplikatoren
• Methode 3 vun 3: Wéi léise ech eng Equatioun mam Diskriminant

An enger kubescher Equatioun ass den héchsten Exponent 3, sou eng Equatioun huet 3 Wuerzelen (Léisungen) an et huet d'Form ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$... E puer Kubikvergläicher sinn net sou einfach ze léisen, awer wann Dir déi richteg Method applizéiert (mat gudden theoreteschen Hannergrond), kënnt Dir d'Wurzele vun och déi komplexste Kubikgleichung fannen - fir dëst benotzt d'Formel fir d'Léisung vun der quadratescher Equatioun ze fannen, ganz Wuerzelen, oder berechent den Diskriminant.

Schrëtt

Method 1 vun 3: Wéi eng kubesch Equatioun ouni konstante Begrëff ze léisen

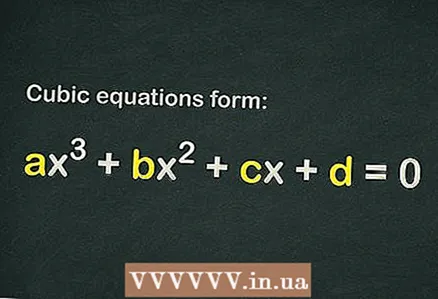1. 1 Fannt eraus ob et e gratis Begrëff an der kubescher Equatioun ass d{ displaystyle d}. Déi kubesch Equatioun huet d'Form ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$... Fir datt eng Equatioun als Kubik ugesi gëtt, ass et genuch datt nëmmen de Begrëff ${ displaystyle x ^ {3}}$ (dat heescht, et gi guer keng aner Memberen).
   • Wann d'Gleichung e gratis Begrëff huet ${ displaystyle d}$, benotzt eng aner Method.
   • Wann an der Equatioun ${ displaystyle a = 0}$, et ass net kubesch.
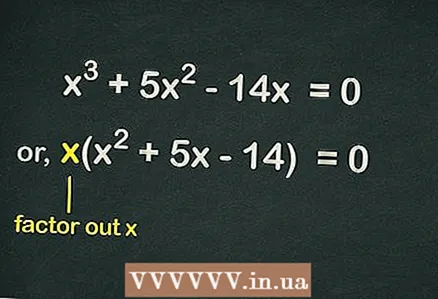2. 2 Huelt aus de Klammern x{ displaystyle x}. Well et kee fräie Begrëff an der Equatioun gëtt, enthält all Begrëff an der Equatioun d'Variabel ${ displaystyle x}$... Dëst bedeit datt een ${ displaystyle x}$ kann aus Klammern ausgeschloss ginn fir d'Gleichung ze vereinfachen. Also gëtt d'Gläichung esou geschriwwen: ${ displaystyle x (ax ^ {2} + bx + c)}$.
   • Zum Beispill, eng kubesch Equatioun uginn ${ Displaystyle 3x ^ {3} -2x ^ {2} + 14x = 0}$
   • Eraushuelen ${ displaystyle x}$ Klammeren a kréien ${ displaystyle x (3x ^ {2} -2x + 14) = 0}$
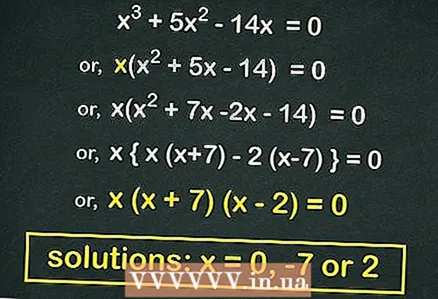3. 3 Faktor (d'Produkt vun zwee Binomien) déi quadratesch Equatioun (wa méiglech). Vill quadratesch Equatioune vun der Form ${ displaystyle ax ^ {2} + bx + c = 0}$ kann faktoriséiert ginn. Sou eng Equatioun wäert erauskommen wa mir eraushuelen ${ displaystyle x}$ ausserhalb vun de Klammeren. An eisem Beispill:
   • Huelt aus de Klammeren ${ displaystyle x}$: ${ displaystyle x (x ^ {2} + 5x-14) = 0}$
   • Faktor der quadratescher Equatioun: ${ Displaystyle x (x + 7) (x-2) = 0}$
   • Gläicht all Këscht un ${ Displaystyle 0}$... D'Wuerzele vun dëser Equatioun sinn ${ Displaystyle x = 0, x = -7, x = 2}$.
4. 4 Léist eng quadratesch Equatioun mat enger spezieller Formel. Maacht dëst wann déi quadratesch Equatioun net faktoriséiert ka ginn. Fir zwou Wuerzelen vun enger Equatioun ze fannen, d'Wäerter vun de Koeffizienten ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ ersetzen an der Formel ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$.
   • An eisem Beispill ersetzen d'Wäerter vun de Koeffizienten ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ (${ displaystyle 3}$, ${ Displaystyle -2}$, ${ displaystyle 14}$) an d'Formel:

     ${ displaystyle { frac {-b pm { sqrt {b ^ {2} -4ac}}} {2a}}}$

     ${ displaystyle { frac {- (- 2) pm { sqrt {((-2) ^ {2} -4 (3) (14)}}} {2 (3)}}}}$

     ${ displaystyle { frac {2 pm { sqrt {4- (12) (14)}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {(4-168}}} {6}}}$

     ${ displaystyle { frac {2 pm { sqrt {-164}}}} {6}}}$

   • Éischt Root:

     ${ displaystyle { frac {2 + { sqrt {-164}}} {6}}}$

     ${ displaystyle { frac {2 + 12,8i} {6}}}$

   • Zweet Root:

     ${ displaystyle { frac {2-12,8i} {6}}}$

5. 5 Benotzt null a quadratesch Wuerzelen als Léisunge fir déi kubesch Equatioun. Quadratesch Equatioune hunn zwou Wuerzelen, wärend kubesch déi dräi hunn. Dir hutt schonn zwou Léisunge fonnt - dat sinn d'Wuerzele vun der quadratescher Equatioun. Wann Dir "x" ausserhalb vun de Klammeren setzt, wier déi drëtt Léisung ${ Displaystyle 0}$.
   • Wann Dir "x" aus de Klammern hëlt, kritt Dir ${ displaystyle x (ax ^ {2} + bx + c) = 0}$, dat heescht zwee Faktoren: ${ displaystyle x}$ an eng quadratesch Equatioun an Klammeren. Wann ee vun dëse Faktoren ass ${ Displaystyle 0}$, déi ganz Equatioun ass och gläich ${ Displaystyle 0}$.
   • Also sinn zwou Wuerzelen vun enger quadratescher Equatioun Léisunge vun enger kubescher Equatioun. Déi drëtt Léisung ass ${ displaystyle x = 0}$.

Method 2 vun 3: Wéi fannt Dir ganz Roots Mat Multiplikatoren

1. 1 Gitt sécher datt et e gratis Begrëff an der Kubikvergläichung ass d{ displaystyle d}. Wann an enger Equatioun vun der Form ${ displaystyle ax ^ {3} + bx ^ {2} + cx + d = 0}$ et gëtt e gratis Member ${ displaystyle d}$ (wat net gläich wéi Null ass), et funktionnéiert net "x" ausserhalb vun de Klammeren ze setzen. An dësem Fall, benotzt d'Method, déi an dëser Sektioun skizzéiert ass.
   • Zum Beispill, eng kubesch Equatioun uginn ${ Displaystyle 2x ^ {3} + 9x ^ {2} + 13x = -6}$... Fir Null op der rietser Säit vun der Equatioun ze kréien, add ${ displaystyle 6}$ op béide Säiten vun der Gleichung.
   • D'Gleichung wäert erauskommen ${ Displaystyle 2x ^ {3} + 9x ^ {2} + 13x + 6 = 0}$... Wéi ${ displaystyle d = 6}$, d'Method, déi an der éischter Sektioun beschriwwe gëtt, kann net benotzt ginn.
2. 2 Schreift d'Faktore vum Koeffizient op a{ displaystyle a} an e gratis Member d{ displaystyle d}. Dat ass, fannt d'Faktore vun der Zuel op ${ displaystyle x ^ {3}}$ an Zuelen virum Gläichzeechen. Denkt drun datt d'Faktore vun enger Zuel d'Zuelen sinn déi, wa se multiplizéiert ginn, dës Zuel produzéieren.
   • Zum Beispill, fir d'Zuel ze kréien 6, Dir musst multiplizéieren ${ Displaystyle 6 mol 1}$ an ${ Displaystyle 2 mol 3}$... Also d'Zuelen 1, 2, 3, 6 si Faktore vun der Zuel 6.
   • An eiser Equatioun ${ displaystyle a = 2}$ an ${ displaystyle d = 6}$... Multiplikatore 2 sinn 1 an 2... Multiplikatore 6 sinn d'Zuelen 1, 2, 3 an 6.
3. 3 Deelt all Faktor a{ displaystyle a} fir all Faktor d{ displaystyle d}. Als Resultat kritt Dir vill Fraktiounen a verschidde ganz Zuelen; d'Wurzelen vun der kubescher Equatioun wäerten ee vun den Ganzer sinn oder den negativen Wäert vun engem vun den Zuelen.
   • An eisem Beispill deelt d'Faktoren ${ displaystyle a}$ (1 an 2) no Faktoren ${ displaystyle d}$ (1, 2, 3 an 6). Dir kritt: ${ Displaystyle 1}$, ${ displaystyle { frac {1} {2}}}$, ${ displaystyle { frac {1} {3}}}$, ${ displaystyle { frac {1} {6}}}$, ${ displaystyle 2}$ an ${ displaystyle { frac {2} {3}}}$... Fügt elo negativ Wäerter vun de kritt Fraktiounen an Zuelen op dës Lëscht: ${ Displaystyle 1}$, ${ Displaystyle -1}$, ${ displaystyle { frac {1} {2}}}$, ${ displaystyle - { frac {1} {2}}}$, ${ displaystyle { frac {1} {3}}}$, ${ displaystyle - { frac {1} {3}}}$, ${ displaystyle { frac {1} {6}}}$, ${ displaystyle - { frac {1} {6}}}$, ${ displaystyle 2}$, ${ Displaystyle -2}$, ${ displaystyle { frac {2} {3}}}$ an ${ displaystyle - { frac {2} {3}}}$... Déi ganz Wuerzele vun der kubescher Equatioun sinn e puer Zuelen aus dëser Lëscht.
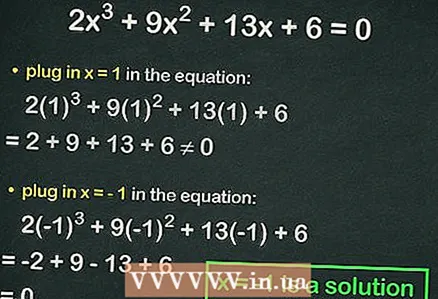4. 4 Plug ganzer Zuelen an d'kubesch Equatioun an. Wann d'Gläichheet richteg ass, ass déi ersetzt Zuel d'Wurzel vun der Equatioun. Zum Beispill, ersetzen an der Gleichung ${ Displaystyle 1}$:
   • ${ displaystyle 2 (1) ^ {3} +9 (1) ^ {2} +13 (1) +6}$ = ${ displaystyle 2 + 9 + 13 + 6}$ ≠ 0, dat heescht, Gläichheet gëtt net beobachtet. An dësem Fall, Plug déi nächst Nummer an.
   • Ersatz ${ Displaystyle -1}$: ${ displaystyle (-2) +9 +(- 13) +6}$ = 0. Also, ${ Displaystyle -1}$ ass déi ganz Wuerzel vun der Gleichung.
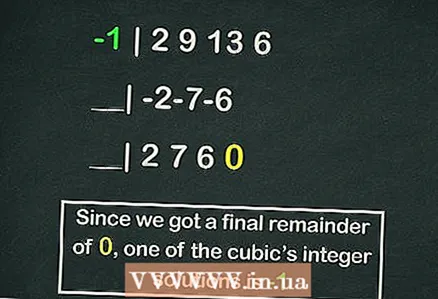5. 5 Benotzt d'Method fir Polynomen ze deelen duerch Schema vum Hornerfir d'Wurzelen vun der Equatioun méi séier ze fannen. Maacht dëst wann Dir keng Nummeren manuell an d'Gleichung wëllt ersetzen. Am Schema vum Horner sinn ganz Zuelen gedeelt duerch d'Wäerter vun de Koeffizienten vun der Equatioun ${ displaystyle a}$, ${ displaystyle b}$, ${ displaystyle c}$ an ${ displaystyle d}$... Wann d'Zuelen gläichméisseg deelbar sinn (dat heescht, de Rescht ass ${ Displaystyle 0}$), eng ganz Zuel ass d'Wurzel vun der Equatioun.
   • Dem Horner säi Schema verdéngt en separaten Artikel, awer dat folgend ass e Beispill fir eng vun de Wuerzelen vun eiser kubescher Equatioun ze berechnen mat dësem Schema:

     -1 | 2 9 13 6

     __| -2-7-6

     __| 2 7 6 0

   • Also de Rescht ass ${ Displaystyle 0}$, awer ${ Displaystyle -1}$ ass eng vun de Wuerzelen vun der Gleichung.

Methode 3 vun 3: Wéi léise ech eng Equatioun mam Diskriminant

1. 1 Schreift d'Wäerter vun de Koeffizienten vun der Gleichung op a{ displaystyle a}, b{ displaystyle b}, c{ displaystyle c} an d{ displaystyle d}. Mir recommandéieren datt Dir d'Wäerter vun den uginnene Koeffizienten am Viraus opschreift fir net an der Zukunft duerchernee ze kommen.
   • Zum Beispill, no der Equatioun ${ Displaystyle x ^ {3} -3x ^ {2} + 3x -1}$... Schreift Iech an ${ displaystyle a = 1}$, ${ displaystyle b = -3}$, ${ displaystyle c = 3}$ an ${ displaystyle d = -1}$... Denkt drun datt wann virdru ${ displaystyle x}$ et gëtt keng Zuel, den entspriechende Koeffizient existéiert nach ëmmer an ass gläich wéi ${ Displaystyle 1}$.
2. 2 Berechent den Null Diskriminant mat enger spezieller Formel. Fir eng Kubik Equatioun mam Diskriminant ze léisen, musst Dir eng Zuel vu schwéiere Berechnunge maachen, awer wann Dir all d'Schrëtt richteg ausféiert, gëtt dës Method onverzichtbar fir déi komplexste Kubik Equatiounen ze léisen. Éischt Berechnung ${ Displaystyle Delta _ {0}}$ (Null Diskriminant) ass deen éischte Wäert dee mir brauchen; Fir dëst ze maachen, ersetzen déi entspriechend Wäerter an der Formel ${ displaystyle Delta _ {0} = b ^ {2} -3ac}$.
   • Den Diskriminant ass eng Zuel déi d'Wurzele vun engem Polynom charakteriséiert (zum Beispill gëtt den Diskriminant vun enger quadratescher Equatioun berechent duerch d'Formel ${ displaystyle b ^ {2} -4ac}$).
   • An eiser Equatioun:

     ${ displaystyle b ^ {2} -3ac}$

     ${ displaystyle (-3) ^ {2} -3 (1) (3)}$

     ${ displaystyle 9-3 (1) (3)}$

     ${ displaystyle 9-9 = 0 = Delta _ {0}}$

3. 3 Berechent den éischten Diskriminant mat der Formel Δ1=2b3−9abc+27a2d{ displaystyle Delta _ {1} = 2b ^ {3} -9abc + 27a ^ {2} d}. Éischt Diskriminant ${ Displaystyle Delta _ {1}}$ - dëst ass den zweete wichtege Wäert; fir et ze berechnen, plug déi entspriechend Wäerter an déi spezifizéiert Formel.
   • An eiser Equatioun:

     ${ displaystyle 2 (-3) ^ {3} -9 (1) (- 3) (3) +27 (1) ^ {2} (- 1)}$

     ${ displaystyle 2 (-27) -9 (-9) +27 (-1)}$

     ${ displaystyle -54 + 81-27}$

     ${ displaystyle 81-81 = 0 = Delta _ {1}}$

4. 4 Berechnen:${ displaystyle Delta = ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div -27a ^ {2}}$... Dat ass, fënnt den Diskriminant vun der kubescher Equatioun duerch déi kritt Wäerter ${ Displaystyle Delta _ {0}}$ an ${ Displaystyle Delta _ {1}}$... Wann den Diskriminant vun enger kubescher Equatioun positiv ass, huet d'Gleichung dräi Wuerzelen; wann den Diskriminant null ass, huet d'Gleichung eng oder zwou Wuerzelen; wann den Diskriminant negativ ass, huet d'Gleichung eng Root.
   • Eng Kubik Gleichung huet ëmmer op d'mannst eng Root, well d'Graf vun dëser Gläichung d'X-Achs op d'mannst op engem Punkt schneit.
   • An eiser Equatioun ${ Displaystyle Delta _ {0}}$ an ${ Displaystyle Delta _ {1}}$ si gläich ${ Displaystyle 0}$, also kënnt Dir ganz einfach berechnen ${ Displaystyle Delta}$:

     ${ displaystyle ( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) div (-27a ^ {2})}}$

     ${ displaystyle ((0) ^ {2} -4 (0) ^ {3}) div (-27 (1) ^ {2})}$

     ${ Displaystyle 0-0 div 27}$

     ${ displaystyle 0 = Delta}$... Also huet eis Equatioun eng oder zwou Wuerzelen.

5. 5 Berechnen:${ displaystyle C = ^ {3} { sqrt { left ({ sqrt { Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}}} + Delta _ {1 } right) div 2}}}$. ${ displaystyle C}$ - dëst ass déi lescht wichteg Quantitéit ze fannen; et hëlleft Iech d'Wurzelen vun der Equatioun ze berechnen. Ersetzen d'Wäerter an déi spezifizéiert Formel ${ Displaystyle Delta _ {1}}$ an ${ Displaystyle Delta _ {0}}$.
   • An eiser Equatioun:

     ${ displaystyle ^ {3} { sqrt {{ sqrt {( Delta _ {1} ^ {2} -4 Delta _ {0} ^ {3}) + Delta _ {1}}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0 ^ {2} -4 (0) ^ {3}) + (0)}} div 2}}}$

     ${ displaystyle ^ {3} { sqrt {{ sqrt {(0-0) +0}} div 2}}}$

     ${ displaystyle 0 = C}$

6. 6 Fannt dräi Wuerzelen vun der Gleichung. Maacht et mat der Formel ${ displaystyle - (b + u ^ {n} C + Delta _ {0} div (u ^ {n} C)) div 3a}$, wou ${ Displaystyle u = (- 1 + { sqrt {-3}}) div 2}$, awer n ass gläich 1, 2 oder 3... Ersetzen déi entspriechend Wäerter an dës Formel - als Resultat kritt Dir dräi Wuerzelen vun der Equatioun.
   • Berechent de Wäert mat der Formel op n = 1, 2 oder 3an da préift d'Äntwert. Wann Dir 0 kritt wann Dir Är Äntwert iwwerpréift, ass dëse Wäert d'Wurzel vun der Equatioun.
   • An eisem Beispill, ersetzen 1 an ${ Displaystyle x ^ {3} -3x ^ {2} + 3x -1}$ a kréien 0, d.h 1 ass eng vun de Wuerzelen vun der Gleichung.