Wéi ze kontrolléieren ob eng Nummer primär ass

Inhalt

Schrëtt
Deel 1 vun 3: Einfachheetstester
Deel 2 vun 3: Wéi Simplicitéit Tester funktionnéieren
Deel 3 vun 3: Benotze vum Chinese Rescht Theorem
Tipps
Wat brauchs du

Primzuelen sinn Zuelen déi nëmme vu sech selwer a mat 1. deelbar sinn. All aner Zuelen ginn zesummegesat Zuelen genannt. Et gi vill Weeër fir festzestellen ob eng Zuel primär ass, a si hunn all hir eege Virdeeler an Nodeeler. Engersäits sinn e puer vun de Methoden ganz korrekt, awer si sinn zimmlech komplex wann Dir mat groussen Zuelen ze dinn hutt. Op der anerer Säit ginn et vill méi séier Weeër, awer si kënnen zu falsche Resultater féieren. D'Wiel vun der passender Method hänkt dovun of wéi grouss d'Zuelen mat deenen Dir schafft.

Schrëtt

Deel 1 vun 3: Einfachheetstester

Note: an all Formelen n bezeechent d'Nummer ze kontrolléieren.

1 Enumeratioun vun Divisoren. Et ass genuch fir ze trennen n op all Primzuelen vun 2 bis zum ofgerënnten Wäert ( ${ Displaystyle { sqrt {n}}}$ ).
2 Dem Fermat säi klengen Theorem. Opgepasst: heiansdo wäert den Test falsch Kompositzuelen als Prime identifizéieren, och fir all Wäerter vun a.
- Loosst eis en Ganzt wielen asou datt 2 ≤ a ≤ n - 1.
- Wann a (mod n) = a (mod n) dann ass d'Zuel wahrscheinlech prim. Wann d'Gläichheet net zefridden ass, ass d'Zuel n zesummegesat.
- Préift déi gegleeft Gläichheet fir verschidde Wäerter afir d'Wahrscheinlechkeet ze erhéijen datt d'Zuel déi getest gëtt wierklech Prime ass.
3 Miller-Rabin Test. Opgepasst: heiansdo, och wann seelen, fir verschidde Wäerter vun a, wäert den Test falsch Kompositzuelen als Prime identifizéieren.
- Fannt d'Quantitéiten s an d sou datt ${ Displaystyle n-1 = 2 ^ {s} * d}$ .
- Wielt eng ganz Zuel a am Beräich 2 ≤ a ≤ n - 1.
- Wann a = +1 (mod n) oder -1 (mod n), dann ass n wahrscheinlech Prime. An dësem Fall, gitt op d'Testresultat. Wann d'Gläichheet net hält, gitt op den nächste Schrëtt.
- Square Är Äntwert ( ${ displaystyle a ^ {2d}}$ ). Wann Dir -1 (Mod n) kritt, dann ass n wahrscheinlech eng Primzuel. An dësem Fall, gitt op d'Testresultat. Wann d'Gläichheet net klappt, widderhuelen ( ${ Displaystyle a ^ {4d}}$ a sou weider) bis ${ displaystyle a ^ {2 ^ {s-1} d}}$ .
- Wann op e puer Schrëtt nodeems Dir eng aner Nummer quadréiert wéi ${ Displaystyle pm 1}$ (Mod n), Dir hutt +1 (Mod n), also n ass eng zesummegesate Zuel. Wann ${ displaystyle a ^ {2 ^ {s-1} d} neq pm 1}$ (mod n), dann ass n net prime.
- Testresultat: wann n den Test passéiert, widderhuelen et fir aner Wäerter afir d'Vertrauen ze erhéijen.

Deel 2 vun 3: Wéi Simplicitéit Tester funktionnéieren

1 Enumeratioun vun Divisoren. Per Definitioun, d'Zuel n ass einfach nëmme wann et net deelbar ass mat 2 an aner ganz Zuelen ausser 1 a sech selwer. Déi uewe genannte Formel erlaabt Iech onnéideg Schrëtt ze läschen an Zäit ze spueren: zum Beispill no der Iwwerpréiwung ob eng Nummer mat 3 deelbar ass, ass et net néideg ze kontrolléieren ob se mat 9 deelbar ass.
- D'Buedem (x) Funktioun ronn x op déi nootste Ganzt manner wéi oder gläich wéi x.
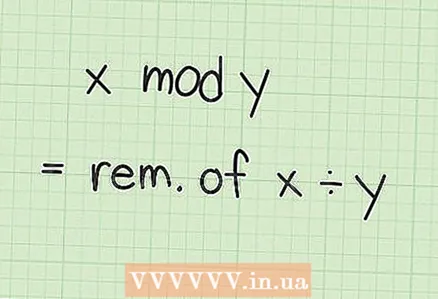2 Léiert iwwer modulär Arithmetik. D'Operatioun "x mod y" (mod ass eng Ofkierzung vum Laténgesche Wuert "modulo", dat heescht "Modul") heescht "deelt x mat y a fënnt de Rescht." An anere Wierder, a modulare Arithmetik, wann Dir e gewësse Wäert erreecht, dee genannt gëtt Modul, d'Zuelen "dréien" erëm op Null. Zum Beispill zielt d'Auer mam Modul 12 of: et weist 10, 11 an 12 Stonnen, an dann zréck op 1.
- Vill Rechner hunn e Mod Schlëssel. D'Enn vun dëser Sektioun weist Iech wéi Dir dës Funktioun fir grouss Zuelen manuell berechent.
3 Léiert iwwer d'Fallfäll vum Fermat's Little Theorem. All Zuelen fir déi d'Testbedéngungen net erfëllt sinn zesummegesat, awer de Rescht vun den Zuelen sinn nëmmen wahrscheinlech sinn einfach. Wann Dir falsch Resultater vermeide wëllt, sicht n an der Lëscht vun "Carmichael Zuelen" (Komposit Zuelen déi dësen Test zefridden stellen) an "Fermat Pseudoprime Zuelen" (dës Zuelen entspriechen den Testbedéngungen nëmme fir e puer Wäerter a).
4 Wann et bequem ass, benotzt de Miller-Rabin Test. Och wann dës Method zimmlech ëmständlech ass fir manuell Berechnungen, gëtt se dacks a Computerprogrammer benotzt. Et bitt akzeptabel Geschwindegkeet a manner Feeler wéi d'Fermat Method. Eng zesummegesate Zuel gëtt net als Primzuel ugeholl wann Berechnunge fir méi wéi ¼ Wäerter ausgefouert ginn a... Wann Dir zoufälleg verschidde Wäerter wielt a a fir si all wäert den Test e positivt Resultat ginn, mir kënne mat engem zimlech héije Grad vu Vertraue dovun ausgoen n ass eng Primzuel.
5 Fir grouss Zuelen, benotzt modulare Arithmetik. Wann Dir kee Mod Rechner praktesch hutt, oder de Rechner net entwéckelt ass fir sou grouss Zuelen ze verschaffen, benotzt Power Properties a modulär Arithmetik fir d'Berechnungen méi einfach ze maachen. Drënner ass e Beispill fir 350{ displaystyle 3 ^ {50}} Mod 50:
- Omschreift den Ausdrock an enger méi praktescher Form: ${ displaystyle (3 ^ {25} * 3 ^ {25})}}$ mod 50. Manuell Berechnunge kënne weider Vereinfachungen erfuerderen.
- ${ displaystyle (3 ^ {25} * 3 ^ {25})}}$ mod 50 = dir ${ displaystyle (3 ^ {25}}$ mod50 ${ displaystyle * 3 ^ {25}}$ mod 50) mod 50. Hei hu mir de Besëtz vun der modulärer Multiplikatioun berécksiichtegt.
- ${ displaystyle 3 ^ {25}}$ Mod 50 = 43.
- ${ displaystyle (3 ^ {25}}$ mod50 ${ displaystyle * 3 ^ {25}}$ mod 50) mod 50 = ${ displaystyle (43 * 43)}$ mod50.
- ${ displaystyle = 1849}$ mod50.
- ${ displaystyle = 49}$ .

Deel 3 vun 3: Benotze vum Chinese Rescht Theorem

1 Wielt zwou Zuelen. Eng vun den Zuelen muss komposit sinn, an déi aner muss genau déi sinn, déi Dir fir Einfachheet testen wëllt.
- Nummer 1 = 35
- Nummer 2 = 97
2 Wielt zwee Wäerter, déi méi grouss si wéi Null a respektiv manner wéi d'Zuelen Number1 an Number2. Dës Wäerter däerfen net déiselwecht sinn.
- Wäert 1 = 1
- Wäert 2 = 2
3 Berechent de MMI (Mathematical Multiplicative Inverse) fir Number1 an Number2.
- Berechent MMI
  - MMI1 = Nummer2 ^ -1 Mod Nummer1
  - MMI2 = Number1 ^ -1 Mod Number2
- Nëmme fir Primzuelen (dëst gëtt eng Zuel fir Komposit Zuelen, awer et wäert net säi MMI sinn):
  - MMI1 = (Number2 ^ (Number1-2))% Number1
  - MMI2 = (Number1 ^ (Number2-2))% Number2
- Zum Beispill:
  - MMI1 = (97 ^ 33)% 35
  - MMI2 = (35 ^ 95)% 97
4 Erstellt en Dësch fir all MMI erof op log2 Moduler:
- Fir MMI1
  - F (1) = Zuel2% Zuel1 = 97% 35 = 27
  - F (2) = F (1) * F (1)% Zuel1 = 27 * 27% 35 = 29
  - F (4) = F (2) * F (2)% Zuel1 = 29 * 29% 35 = 1
  - F (8) = F (4) * F (4)% Zuel1 = 1 * 1% 35 = 1
  - F (16) = F (8) * F (8)% Zuel1 = 1 * 1% 35 = 1
  - F (32) = F (16) * F (16)% Zuel1 = 1 * 1% 35 = 1
- Berechent Paired Numbers 1 - 2
  - 35 -2 = 33 (10001) Basis 2
  - MMI1 = F (33) = F (32) * F (1) mod 35
  - MMI1 = F (33) = 1 * 27 Mod 35
  - MMI1 = 27
- Fir MMI2
  - F (1) = Zuel1% Zuel2 = 35% 97 = 35
  - F (2) = F (1) * F (1)% Zuel2 = 35 * 35 Mod 97 = 61
  - F (4) = F (2) * F (2)% Number2 = 61 * 61 mod 97 = 35
  - F (8) = F (4) * F (4)% Number2 = 35 * 35 mod 97 = 61
  - F (16) = F (8) * F (8)% Zuel2 = 61 * 61 Mod 97 = 35
  - F (32) = F (16) * F (16)% Zuel2 = 35 * 35 Mod 97 = 61
  - F (64) = F (32) * F (32)% Zuel2 = 61 * 61 Mod 97 = 35
  - F (128) = F (64) * F (64)% Zuel2 = 35 * 35 Mod 97 = 61
- Berechent d'Paired Number 2 - 2
  - 97 - 2 = 95 = (1011111) Basis 2
  - MMI2 = (((((F (64) * F (16)% 97) * F (8)% 97) * F (4)% 97) * F (2)% 97) * F) (1)% 97)
  - MMI2 = (((((35 * 35)% 97) * 61)% 97) * 35% 97) * 61% 97) * 35% 97)
  - MMI2 = 61
5 Berechnen (Value1 * Number2 * MMI1 + Value2 * Number1 * MMI2)% (Number1 * Number2)
- Äntwert = (1 * 97 * 27 + 2 * 35 * 61)% (97 * 35)
- Äntwert = (2619 + 4270)% 3395
- Äntwert = 99
6 Préift ob d'Nummer1 net primär ass
- Berechnen (Äntwert - Wäert1)% Zuel1
- 99 – 1 % 35 = 28
- Well 28 méi grouss ass wéi 0, ass 35 keng Primzuel.
7 Préift ob d'Nummer 2 primär ass.
- Berechent (Äntwert - Wäert2)% Zuel2
- 99 – 2 % 97 = 0
- Well 0 0 ass, ass 97 héchstwahrscheinlech eng Primzuel.
8 Widderhuelen Schrëtt 1 bis 7 op d'mannst zwee Mol méi.
- Wann Dir 0 am Schrëtt 7 kritt:
  - Benotzt eng aner Nummer1 wann d'Nummer1 net priem ass.
  - Benotzt eng aner Nummer1 wann d'Nummer1 primär ass. An dësem Fall sollt Dir 0 a Schrëtt 6 a 7 kréien.
  - Benotzt verschidde Bedeitung1 a Bedeitung2.
- Wann Dir am Schrëtt 7 konsequent 0 kritt, dann ass d'Nummer 2 ganz wahrscheinlech Prime.
- Schrëtt 1 bis 7 kënnen zu engem Feeler féieren wann d'Nummer1 net primär ass an d'Nummer2 en Divisor vun der Nummer1 ass. Déi beschriwwen Method funktionnéiert an alle Fäll wa béid Zuelen primär sinn.
- De Grond datt Dir Schrëtt 1 bis 7 musst widderhuelen ass well an e puer Fäll, och wann d'Nummer1 an d'Nummer 2 net priem sinn, kritt Dir am Schrëtt 7 0 (fir eng oder béid Zuelen). Dëst geschitt selten.Wielt eng aner Nummer1 (Komposit), a wann d'Nummer2 net priem ass, dann ass d'Nummer2 net gläich wéi Null am Schrëtt 7 (ausser de Fall wann d'Nummer1 en Divisor vun der Nummer 2 ass - hei sinn Primen ëmmer gläich wéi Null am Schrëtt 7).

Tipps

Primzuelen vun 168 op 1000: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, 47, 53, 59, 61, 67, 71, 73, 79 , 83, 89, 97, 101, 103, 107, 109, 113, 127, 131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199, 211 , 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283, 293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359 , 367, 373, 379, 383, 389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467, 479, 487, 491, 499, 503, 509 , 521, 523, 541, 547, 557, 563, 569, 571, 577, 587, 593, 599, 601, 607, 613, 617, 619, 631, 641, 643, 647, 653, 659, 661, 673 , 677, 683, 691, 701, 709, 719, 727, 733, 739, 743, 751, 757, 761, 769, 773, 787, 797, 809, 811, 821, 823, 827, 829, 839, 853 , 857, 859, 863, 877, 881, 883, 887, 907, 911, 919, 929, 937, 941, 947, 953, 967, 971, 977, 983, 991, 997.
Och wa brute Kraaft Testen en langweilegen Test ass wann Dir mat groussen Zuelen schafft, ass et zimmlech effizient fir kleng Zuelen. Och am Fall vu groussen Zuelen, fänkt un mat klengen Divisoren ze testen, a gitt dann op méi raffinéiert Methoden fir d'Einfachheet vun Zuelen ze kontrolléieren (wa kleng Divisoren net fonnt ginn).