Inhalt

• Schrëtt
• Method 1 vun 6: D'Basics
• Method 2 vun 6: Domain vu Fraktiounsfunktiounen
• Method 3 vun 6: Ëmfang vun enger gewurzter Funktioun
• Method 4 vun 6: Domain vun enger natierlecher Logarithmus Funktioun
• Method 5 vun 6: Fannt eng Domain Mat engem Plot
• Method 6 vun 6: Fannt eng Domain Mat engem Set

E Funktiounsdomän ass eng Rei vun Zuelen op deenen eng Funktioun definéiert ass. An anere Wierder, dëst sinn d'Wäerter vun x déi an déi uginn Equatioun ersat kënne ginn. Déi méiglech Wäerter vun y ginn d'Bereich vun der Funktioun genannt. Wann Dir den Ëmfang vun enger Funktioun a verschiddene Situatioune wëllt fannen, befollegt dës Schrëtt.

Schrëtt

Method 1 vun 6: D'Basics

1. 1 Denkt drun wat eng Domain ass. Den Domain vun der Definitioun ass de Set vu Wäerter vun x, wa se an d'Gleichung ersat ginn, kréien mir d'Gamme vu Wäerter vun y.
2. 2 Léiert d'Domain vu verschiddene Funktiounen ze fannen. D'Funktiounstyp bestëmmt d'Method fir den Ëmfang ze fannen. Hei sinn d'Haaptpunkte déi Dir iwwer all Zort Funktioun wësse sollt, déi an der nächster Sektioun diskutéiert ginn:
   • Polynom Funktioun ouni Wuerzelen oder Variabelen am Nenner. Fir dës Zort Funktioun ass den Ëmfang all reell Zuelen.
   • Fraktiounsfunktioun mat Variabel am Nenner. Fir d'Domain vun enger bestëmmter Aart Funktioun ze fannen, gläichstellt den Nenner mat Null an ausschléisst déi fonnt Wäerter vun x.
   • Funktioun mat enger Variabel an der Root. Fir den Ëmfang vun enger bestëmmter Funktiounstyp ze fannen, spezifizéiert e Radikal méi grouss wéi oder gläich wéi 0 a fënnt d'x Wäerter.
   • Natierlech Logarithmus Funktioun (ln). Gitt den Ausdrock ënner dem Logarithmus> 0 a léisen.
   • Zäitplang. Zeechnen eng Grafik fir x ze fannen.
   • Eng Rëtsch vun. Dëst wäert eng Lëscht vun x an y Koordinaten sinn. D'Definitiounsberäich ass eng Lëscht mat x Koordinaten.
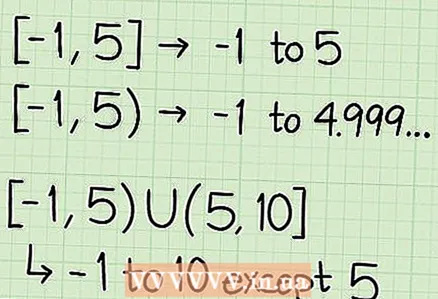3. 3 Markéiert d'Definitiounsberäich korrekt. Et ass einfach ze léieren wéi een d'Domain vun der Definitioun korrekt markéiert, awer et ass wichteg datt Dir d'Äntwert richteg opschreift an héich Punkte kritt. Hei sinn e puer Saachen déi Dir wësse sollt iwwer d'Schreiwen vun engem Ëmfang:
   • Ee vun de Formater fir den Ëmfang vun der Definitioun ze schreiwen: Quadratklammer, 2 Ennwäerter vum Ëmfang, Ronn Klammer.
     • Zum Beispill, [-1; fënnef). Dëst bedeit e Beräich vun -1 bis 5.
   • Benotzt quadratesch Klammern [ an ] fir unzeginn datt de Wäert am Ëmfang ass.
     • Also, am Beispill [-1; 5) d'Géigend enthält -1.
   • Benotzt Klammern ( an ) fir unzeginn datt de Wäert net am Ëmfang ass.
     • Also, am Beispill [-1; 5) 5 gehéiert net zu der Regioun. Den Ëmfang enthält nëmme Wäerter onendlech no bei 5, dat heescht 4.999 (9).
   • Benotzt d'U U Zeechen fir Gebidder ze kombinéieren getrennt vun engem Spalt.
     • Zum Beispill, [-1; 5) U (5; 10]. Dëst bedeit datt d'Regioun vun -1 op 10 inklusiv geet, awer net enthält 5. Dëst kann fir eng Funktioun sinn wou den Nenner "x - 5" ass.
     • Dir kënnt multiple Us benotze wéi néideg wann d'Géigend multiple Lücken / Lücken huet.
   • Benotzt d'Plus Infinity a Minus Infinity Zeechen fir auszedrécken datt d'Géigend onendlech an all Richtung ass.
     • Benotzt ëmmer () anstatt [] mat engem Infinity Zeechen.

Method 2 vun 6: Domain vu Fraktiounsfunktiounen

1. 1 Schreift e Beispill. Zum Beispill kritt Dir déi folgend Funktioun:
   • f (x) = 2x / (x - 4)
2. 2 Fir Fraktiounsfunktiounen mat enger Variabel am Nenner muss den Nenner op Null ausgeglach ginn. Wann Dir den Domain vun der Definitioun vun enger Fraktiounsfunktioun fënnt, ass et noutwendeg all Wäerter vun x auszeschléissen, bei deenen den Nenner null ass, well Dir kënnt net mat Null deelen. Schreift den Nenner als Equatioun op a set se gläich op 0. Hei ass wéi et ze maachen:
   • f (x) = 2x / (x - 4)
   • x - 4 = 0
   • (x - 2) (x + 2) = 0
   • x ≠ 2; dir. - 2
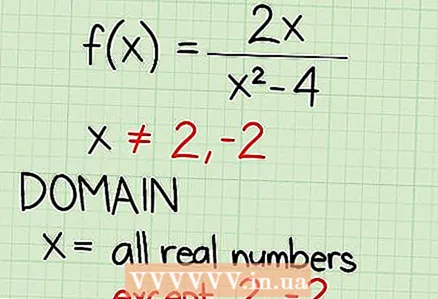3. 3 Schreift den Ëmfang op:
   • x = all reell Zuelen ausser 2 an -2

Method 3 vun 6: Ëmfang vun enger gewurzter Funktioun

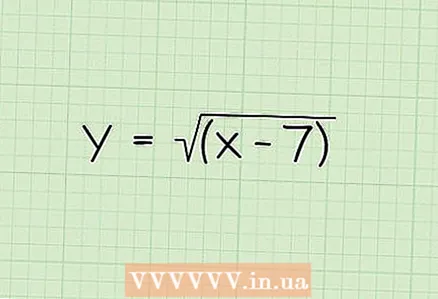1. 1 Schreift e Beispill. Gitt eng Funktioun y = √ (x-7)
2. 2 Setzt de radikalen Ausdrock op méi wéi oder gläich wéi 0. Dir kënnt de Quadratwurzel vun enger negativer Zuel net extrahieren, och wann Dir de Quadratwuerzel vun 0. extrahéiere kënnt. Also, setzt de radikalen Ausdrock méi grouss wéi oder gläich op 0. Notéiert datt dëst net nëmme fir Quadratwurzelen gëllt, awer och fir all Wuerzelen mat e gläiche Grad. Wéi och ëmmer, dëst gëllt net fir Wuerzelen mat engem komeschen Grad, well eng negativ Zuel kann ënner enger komescher Wuerzel optrieden.
   • x - 7 ≧0
3. 3 Highlight d'Variabel. Fir dëst ze maachen, réckelt 7 op déi riets Säit vun der Ongläichheet:
   • x ë 7
4. 4 Schreift den Ëmfang op. Do ass hatt:
   • D = [7; + ∞)
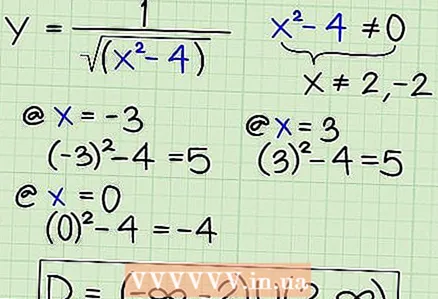5. 5 Fannt den Ëmfang vun enger rootéierter Funktioun wann et verschidde Léisunge gëtt. Gitt: y = 1 / √ (̅x -4). Den Nenner op Null ze setzen an dës Equatioun ze léisen gëtt Iech x ≠ (2; -2). Hei ass wéi Dir weidergeet:
   • Préift d'Gebitt iwwer -2 (zum Beispill, ersetzen -3) fir sécherzestellen datt Ersatz Zuelen manner wéi -2 am Nenner zu enger Zuel méi grouss wéi 0. An esou:
     • (-3) - 4 = 5
   • Préift elo d'Géigend tëscht -2 an +2. Ersatz 0 zum Beispill.
     • 0 -4 = -4, sou datt d'Zuelen tëscht -2 an 2 net funktionnéieren.
   • Probéiert elo Zuelen méi grouss wéi 2, wéi 3.
     • 3 - 4 = 5, also Zuelen méi grouss wéi 2 si gutt.
   • Schreift den Ëmfang op. Dëst ass wéi dëst Gebitt geschriwwe gëtt:
     • D = (-∞; -2) U (2; + ∞)

Method 4 vun 6: Domain vun enger natierlecher Logarithmus Funktioun

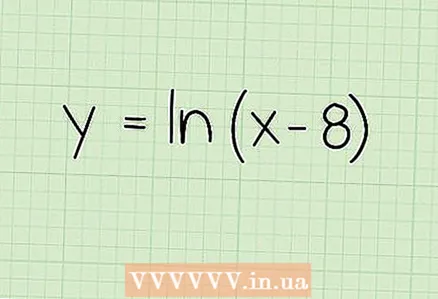1. 1 Schreift e Beispill. Loosst eis soen datt d'Funktioun gëtt:
   • f (x) = ln (x - 8)
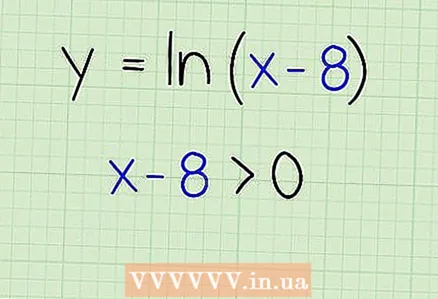2. 2 Spezifizéiert den Ausdrock ënner dem Logarithmus méi grouss wéi Null. Den natierleche Logarithmus muss eng positiv Zuel sinn, sou datt mir den Ausdrock bannent de Klammeren op méi grouss wéi Null setzen.
   • x - 8> 0
3. 3 Entscheet. Fir dëst ze maachen, isoléiert d'Variabel x andeems 8 op béid Säiten vun der Ongläichheet bäidréit.
   • x - 8 + 8> 0 + 8
   • x> 8 an
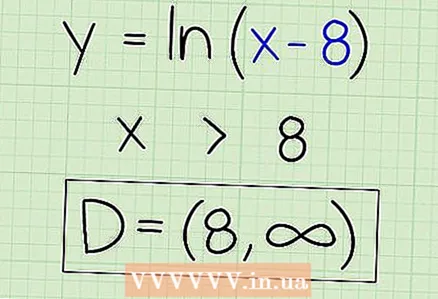4. 4 Schreift den Ëmfang op. Den Ëmfang vun dëser Funktioun ass all Zuel méi grouss wéi 8. Esou:
   • D = (8; + ∞)

Method 5 vun 6: Fannt eng Domain Mat engem Plot

1. 1 Kuckt Iech d'Grafik un.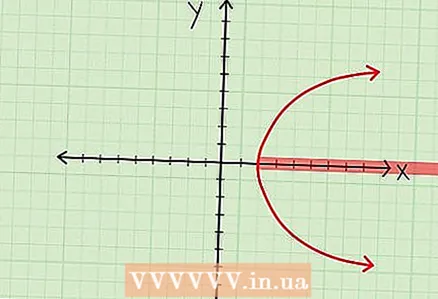
2. 2 Préift d'x Wäerter, déi op der Grafik ugewise ginn. Dëst kann méi einfach gesot wéi gemaach sinn, awer hei sinn e puer Tipps:
   • Linn. Wann Dir eng Zeil um Diagramm gesitt, déi op d'Onendlechkeet geet, dann all d'x Wäerter si richteg an den Ëmfang enthält all reell Zuelen.
   • Eng gewéinlech Parabel. Wann Dir eng Parabel kuckt, déi no uewen oder erof kuckt, dann ass den Ëmfang all reell Zuelen, well all Zuelen op der x-Achs passen.
   • Läit Parabel. Elo, wann Dir eng Parabel mat Apex um Punkt (4; 0) hutt, deen onendlech no riets erstreckt, dann ass d'Domain D = [4; + ∞)
3. 3 Schreift den Ëmfang op. Schreift den Ëmfang of op Basis vun der Aart vun der Grafik mat där Dir schafft. Wann Dir net sécher sidd iwwer den Typ vun der Grafik an Dir wësst d'Funktioun déi se beschreift, plugg d'x Koordinaten an d'Funktioun fir ze testen.

Method 6 vun 6: Fannt eng Domain Mat engem Set

1. 1 Schreift de Set op. E Set ass eng Sammlung vu x an y Koordinaten. Zum Beispill schafft Dir mat de folgende Koordinaten: {(1; 3), (2; 4), (5; 7)}
2. 2 Schreift d'x koordinéiert. Dëst ass 1; 2; fënnef.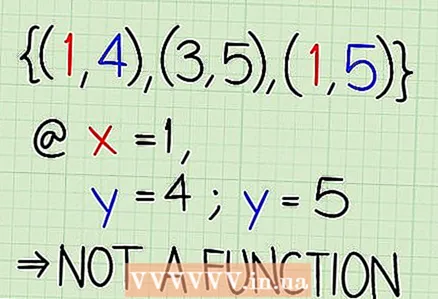
3. 3 Domain: D = {1; 2; fënnef}
4. 4 Gitt sécher datt de Set eng Funktioun ass. Dëst erfuerdert datt all Kéier wann Dir de Wäert fir x ersetzt, kritt Dir dee selwechte Wäert fir y. Zum Beispill, x = 3 ersetzen, sollt Dir y = 6 kréien, a sou weider. De Set am Beispill ass keng Funktioun, well zwee verschidde Wäerter ginn op: {(1; 4), (3; 5), (1; 5)}.