Inhalt

• Schrëtt
• Berodung

Wann Dir e Mathematiker oder e Grafiker ass, musst Dir wahrscheinlech de Wénkel tëscht zwee gegebene Vektoren fannen. An dësem Artikel weist wikiHow Iech wéi een dat maache kann.

Schrëtt

Deel 1 vun 2: Fannt de Wénkel tëscht zwee Vektoren

1. 

   Vektordefinitioun. Schreift all d'Informatiounen iwwer déi zwee Vektoren déi Dir hutt. Stellt Iech vir datt Dir nëmmen déi spezifizéiert Parameteren vun hiren Dimensiounskoordinaten hutt (och Komponente genannt). Wann Dir d'Längt (Magnitude) vun engem Vektor scho wësst, kënnt Dir e puer vun de Schrëtt hei drënner sprangen.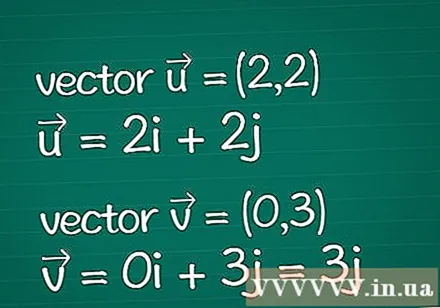
   • Beispill: Zweedimensional Vecteur = (2,2) an zweedimensional Vecteur = (0,3). Si kënnen och als = 2 geschriwwe ginnech + 2j an = 0ech + 3j = 3j.
   • Och wa zweedimensional Vecteure am Beispill an dësem Artikel benotzt ginn, kënnen déi folgend Instruktioune fir Vecteure mat enger Zuel vun Dimensioune gëllen.

2. 

   
   
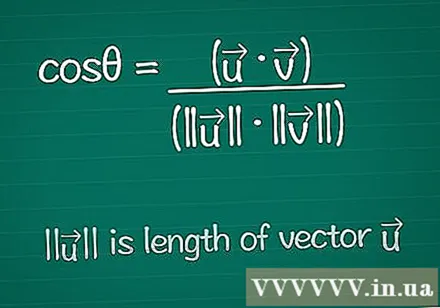
   Schreift d'Kosinusformel op. Fir de Wénkel find tëscht zwee Vektoren ze fannen, fänke mir mat der Formel fir de Kosinus fir dee Wénkel ze fannen. Dir kënnt iwwer dës Formel hei ënnen léieren, oder se einfach esou opschreiwen:
   • cosθ = (•) / (|||| ||||)
   • |||| heescht "Längt vum Vektor".
   • • ass de scalaresche Produkt vun deenen zwee Vektoren - dëst gëtt hei ënnendrënner erkläert.

3. 

   
   
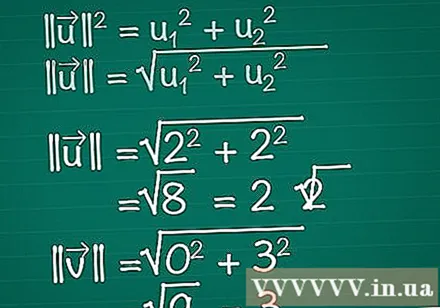
   Berechent d'Längt vun all Vecteure. Stellt Iech vir, e richtegen Dräieck besteet aus den x, y Komponente vum Vektor, an dem Vektor selwer. De Vecteur bildet d'Hypotenus vum Dräieck, fir seng Längt ze fannen benotze mir de Pythagoras-Theorem. Tatsächlech kann dës Formel einfach op e Vektor vun all Zuel vun Dimensiounen erweidert ginn.
   • || u || = u₁ + u₂. Wann e Vektor méi wéi zwee Elementer huet, musst Dir just weider + u addéieren₃ + u₄ +...
   • Dofir fir en zweedimensional Vecteure, || u || = √ (u₁ + u₂).
   • An dësem Beispill, |||| = √ (2 + 2) = √ (8) = 2√2. |||| = √(0 + 3) = √(9) = 3.

4. 

   
   
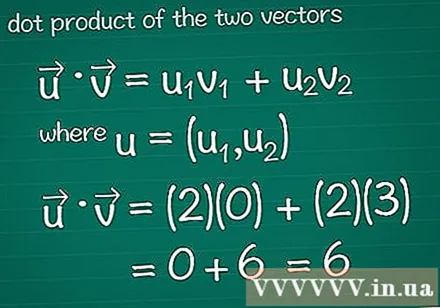
   Berechent de scalaresche Produkt vun zwee Vektoren. Vläicht hutt Dir d'Method vun der Vektormultiplikatioun geléiert, och bekannt als scalar dëst. Fir de skalare Produkt relativ zu hirer Zesummesetzung ze berechnen, multiplizéieren d'Ingredienten an all Richtung zesummen, da füügt dat ganzt Resultat zesummen.
   • Fir de Grafikprogramm fannt Dir Tipps ier Dir weider liest.
   • An der Mathé • = u₁v₁ + u₂v₂, wou, u = (u₁, u₂). Wann de Vektor méi wéi zwee Elementer huet, füügt einfach + u bäi₃v₃ + u₄v₄...
   • An dësem Beispill, • = u₁v₁ + u₂v₂ = (2)(0) + (2)(3) = 0 + 6 = 6. Dëst ass de skalare Produkt vum Vektor a vum Vektor.

5. 

   Setzt d'Resultater an d'Formel. Denkt drun datt cosθ = (•) / (|||| || ||). Elo wësse mer souwuel de skalare Produkt an d'Längt vun all Vektor. Gitt dës an d'Formel fir de Kosinus vum Wénkel auszerechnen.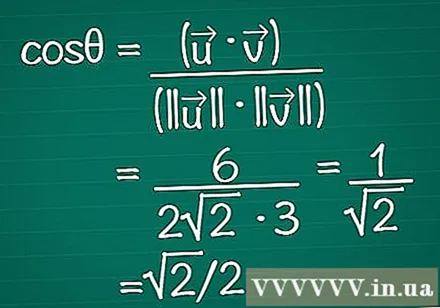
   • An eisem Beispill, cosθ = 6 / (2√2 * 3) = 1 / √2 = √2 / 2.

6. 

   Fannt de Wénkel baséiert op sengem Kosinus. Dir kënnt d'Arccos oder d'Cos-Funktioun an engem Rechner benotze fir θ aus engem bekannte Cos-Wäert ze fannen. Mat e puer Resultater kënnt Dir de Wénkel op Basis vum Eenheetskrees fannen.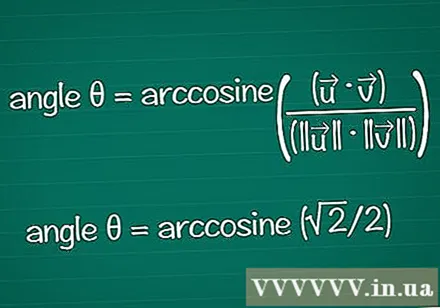
   • Am Beispill cosθ = √2 / 2. Gitt "Arccos (√2 ​​/ 2)" an Ärem Rechner fir de Wénkel ze fannen. Oder Dir fannt de Wénkel θ um Eenheetskrees, op der Positioun cosθ = √2 / 2. Et ass richteg fir θ = /₄ oder 45º.
   • Alles kombinéiert ass d'Finale Formel: Wénkel θ = Arkkosin ((•) / (|||| || ||))
   Annonce

Deel 2 vun 2: Bestëmmung vun der Wénkelformel

1. 

   Den Zweck vun der Formel verstoen. Dës Formel gouf net vu existente Regelen ofgeleet. Amplaz datt et als Definitioun vum skalare Produkt an de Wénkel tëscht den zwee Vektoren geformt gëtt. Trotzdem war et keng arbiträr Entscheedung. Zréckgoen op Basisgeometrie, kënne mir verstoen firwat dës Formel intuitiv an nëtzlech Definitiounen ubitt.
   • D'Beispiller hei ënnendrënner benotze zweedimensional Vektoren well se am einfachsten ze verstoen an am einfachsten sinn. Dräi-zweedimensional oder méi Vektoren hunn Eegeschafte definéiert duerch bal ähnlech allgemeng Formelen.

2. 

   Kritik vum Cosine sengem Theorem. Betruecht en normale Dräieck mat Wénkel θ tëscht de Säiten a a b, dergéint Säit c. De Cosine Theorem seet datt c = a + b -2abcos(θ). Dëst Resultat gëtt ganz einfach aus Basisgeometrie gezunn.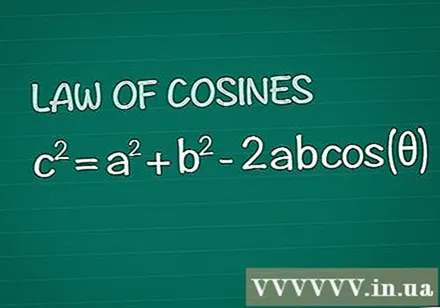

3. 

   Verbannt zwee Vektoren, bilden en Dräieck. Zeechent e puer zweedimensional Vektoren op Pabeier, Vektoren a Vektoren, woubäi the de Wénkel tëscht hinnen ass. Zeechent en drëtte Vektor tëscht dësen zwee fir en Dräieck ze kreéieren. An anere Wierder, zitt e Vektor sou datt + =. Vektor = -.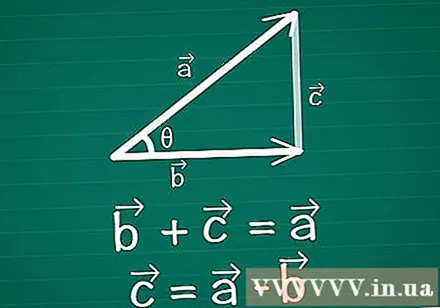

4. 

   Schreift de Cosine Theorem fir dësen Dräieck. Ersetzt d'Säitelängt vun eisem "Vektordräieck" an de Cosine Theorem:
   • || (a - b) || = || a || + || b || - 2 || a || || b ||cos(θ)

5. 

   Nees mat engem scalar Produkt ëmschreiwen. Denkt drun, e skalar Produkt ass d'Bild vun engem Vecteur op deem aneren. De scalaresche Produkt vun engem Vektor mat sech selwer erfuerdert keng Projektioun, well hei ass et keen Ënnerscheed an der Richtung. Dat heescht • = || a ||. Mat dësem iwwerschreiwe mir d'Equatioun:
   • (-) • (-) = • + • - 2 || a || || b ||cos(θ)

6. 

   Erfollegräich déiselwecht Formel nei geschriwwen. Erweidert déi lénks Säit vun der Formel, da vereinfacht d'Formel benotzt fir Wénkelen ze fannen.
   • • - • - • + • = • + • - 2 || a || || b ||cos(θ)
   • - • - • = -2 || a || || b ||cos(θ)
   • -2 (•) = -2 || a || || b ||cos(θ)
   • • = || a || || b ||cos(θ)
   Annonce

Berodung

• Fir Wäerter z'änneren an de Problem séier ze léisen, benotzt dës Formel fir all zweedimensional Vektoren: cosθ = (u₁ • v₁ + u₂ • v₂) / (√ (u₁ • u₂) • √ (v₁ • v₂)).
• Wann Dir mat Computergrafiksoftware schafft, ass d'Chance datt Dir nëmmen ëm d'Vektoren Dimensioun këmmert ouni Iech iwwer hir Längt ze këmmeren. Benotzt déi folgend Schrëtt fir eng Gleichung ze verkierzen an Äre Programm ze beschleunegen:
  • Normaliséier all Vecteure sou datt se gläich sinn 1. Fir dëst ze maachen, deelt all Vecteure Komponent duerch seng Längt.
  • Kritt de normaliséierte Produkt vum Skalar amplaz vum Originalvektor.
  • Well d'Längt 1 ass, kënne mir d'Längtelementer aus der Gleichung ausschléissen. Schlussendlech ass d'Wénkelequatioun Arccos (•).
• Baséierend op der Kosinusformel kënne mir séier feststellen ob de Wénkel akut oder stomp ass. Fänkt mat cosθ = (•) / (|||| ||||) un:
  • Déi lénks a riets Säit vun der Gleichung mussen datselwecht Zeechen hunn (positiv oder negativ).
  • Well d'Längt ëmmer positiv ass, muss cosθ datselwecht Zeechen hunn wéi dat scalar Produkt.
  • Dofir, wann d'Produkt positiv ass, ass cosθ och positiv. Mir sinn am éischte Quadrant vum Eenheetskrees, mat θ <π / 2 oder 90º. De Wénkel fir ze fannen ass de schaarfe Wénkel.
  • Wann de skalare Produkt negativ ass, ass cosθ negativ. Mir sinn am zweete Quadrant vum Eenheetskrees, mat π / 2 <θ ≤ π oder 90º <θ ≤ 180º. Dat ass de Prisongshorn.