Inhalt

• Schrëtt
• Tipps

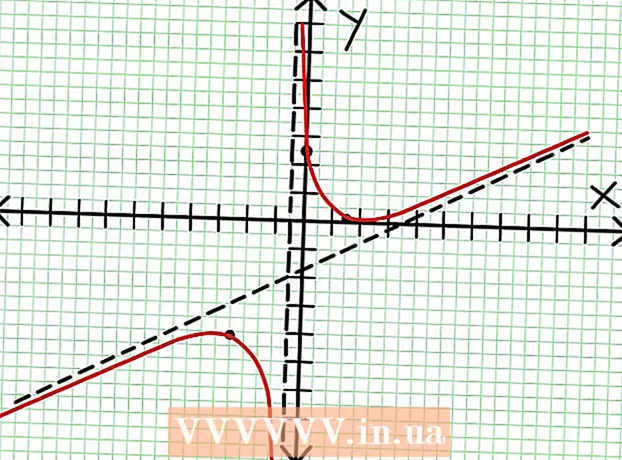
Déi rational Funktioun huet d'Form y = N (x) / D (x), wou N an D Polynome sinn. Fir sou eng Funktioun präzis ze plangen, braucht Dir e gutt Wëssen vun der Algebra, inklusiv Differenzialberechnungen. Betruecht dat folgend Beispill: y = (2x - 6x + 5)/(4x + 2).

Schrëtt

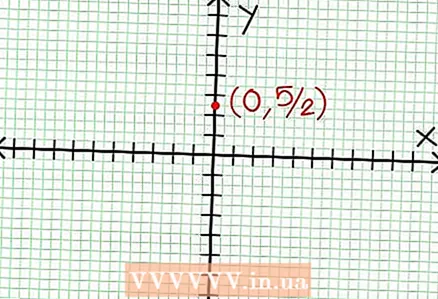1. 1 Fannt den y-Intercept vun der Graf. Fir dëst ze maachen, ersetzt x = 0 an d'Funktioun a kritt y = 5/2. Also huet de Schnëttpunkt vun der Graf mat der Y Achs Koordinaten (0, 5/2).Setzt dëse Punkt op der Koordinatefliger.
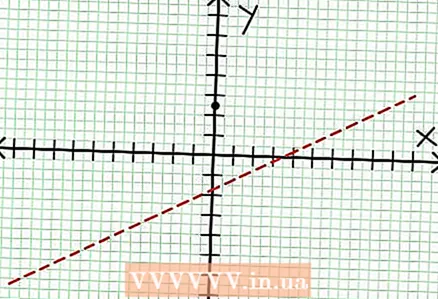2. 2 Fannt déi horizontal Asymptoten. Deelt den Teller mam Nenner (an enger Kolonn) fir d'Verhalen vun "y" mat Wäerter vun "x" ze bestëmmen déi onendlech tendéieren. An eisem Beispill wäert d'Divisioun sinn y = (1/2)x - (7/4) + 17/(8x + 4). Fir grouss positiv oder negativ Wäerter vun "x" 17 / (8x + 4) tendéiert op Null, an d'Grafik Approche déi riicht Linn vun der Funktioun y = (1/2)x - (7/4). Benotzt déi gestippte Linn, plott dës Funktioun.
   • Wann de Grad vum Teller manner ass wéi de Grad vum Nenner, da kënnt Dir den Teller net mam Nenner deelen an den Asymptote gëtt vun der Funktioun beschriwwen op = 0.
   • Wann de Grad vum Teller gläich mam Grad vum Nenner ass, ass den Asymptote eng horizontal Linn gläich wéi de Verhältnis vun de Koeffizienten op "x" am héchsten Grad.
   • Wann de Grad vum Teller 1 méi ass wéi de Grad vum Nenner, dann ass den Asymptote eng schréiegt riicht Linn, där hir Hang gläich ass mam Verhältnis vun de Koeffizienten op "x" zum héchsten Grad.
   • Wann de Grad vum Teller méi grouss ass wéi de Grad vum Nenner mat 2, 3, etc., dann fir grouss Wäerter |NS| Bedeitung op tendéieren onendlech (positiv oder negativ) a Form vun engem Quadrat, kubesche oder aneren Grad vun engem Polynom. An dësem Fall, héchstwahrscheinlech, braucht Dir keng exakt Graf vun der Funktioun ze bauen, déi kritt gëtt andeems Dir den Teller mam Nenner deelt.
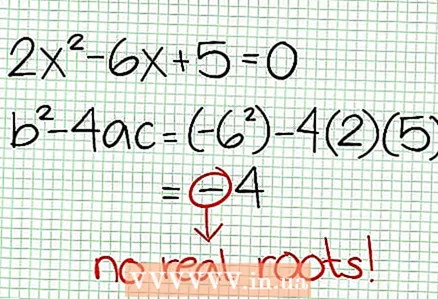3. 3 Fannt d'Nullen vun der Funktioun. Eng rational Funktioun huet Nullen wann säin Teller null ass, dat heescht N (NS) = 0. An eisem Beispill, 2x - 6x + 5 = 0. Den Diskriminant vun dëser quadratescher Equatioun: b - 4ac = 6 - 4 * 2 * 5 = 36 - 40 = -4. Well den Diskriminant negativ ass, dann N (NS), an dofir F (NS) huet keng richteg Wuerzelen. D'Grafik vun enger rationaler Funktioun schneit d'X-Achs net. Wann d'Funktioun Nullen (Wuerzelen) huet, da setzt se op d'Koordinatefliger.
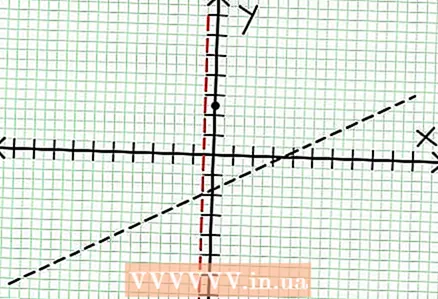4. 4 Fannt déi vertikal Asymptoten. Fir dëst ze maachen, set den Nenner op Null. An eisem Beispill, 4x + 2 = 0 an NS = -1/2. Plot déi vertikal Asymptote mat der gestippter Linn. Wann fir e puer Wäert NS N (NS) = 0 an D (NS) = 0, dann existéiert déi vertikal Asymptote entweder oder existéiert net (dëst ass e rare Fall, awer et ass besser et z'erënneren).
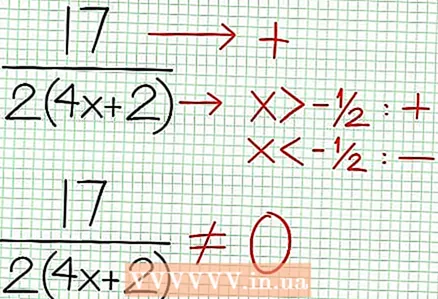5. 5 Kuckt de Rescht vum Teller gedeelt duerch den Nenner. Ass et positiv, negativ oder null? An eisem Beispill ass de Rescht 17, wat positiv ass. Nenner 4x + 2 positiv riets vun der vertikaler Asymptote an negativ lénks dovun. Dëst bedeit datt d'Graf vun der rationaler Funktioun fir grouss positiv Wäerter NS Approche den Asymptote vun uewen, a fir grouss negativ Wäerter NS - vun ënnen. Zënter 17 / (8x + 4) ass ni gläich wéi Null, da wäert d'Graf vun dëser Funktioun ni déi direkt Linn, déi vun der Funktioun uginn ass, schneiden op = (1/2)NS - (7/4).
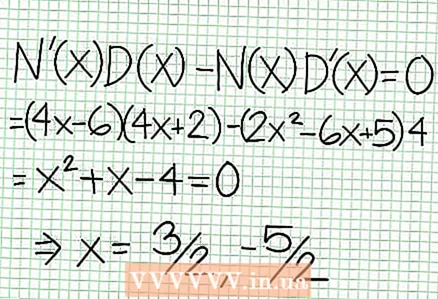6. 6 Fannt lokal Extrem. E lokale Extremum existéiert fir N '(x) D (dirx) - N (dir.x) D '(dirx) = 0. An eisem Beispill, N '(x) = 4x - 6 und D '(x) = 4. N '(x) D (dirx) - N (dir.x) D '(dirx) = (4x - 6)(4x + 2) - (2x - 6x + 5)*4 = x + x - 4 = 0. Dës Equatioun ze léisen, Dir fannt dat x = 3/2 an x = -5/2. (Dëst sinn net ganz korrekt Wäerter, awer si si gëeegent fir eise Fall wann Iwwerpräzis net gebraucht gëtt.)
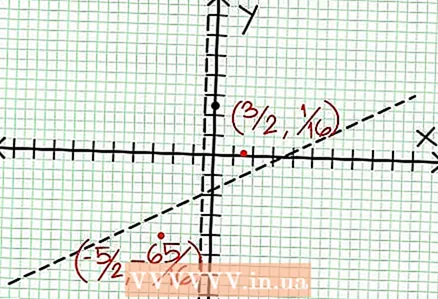7. 7 Fannt de Wäert op fir all lokal Extrem. Fir dëst ze maachen, ersetzen d'Wäerter NS an déi ursprénglech rational Funktioun. An eisem Beispill, f (3/2) = 1/16 an f (-5/2) = -65/16. Setzt Punkten (3/2, 1/16) an (-5/2, -65/16) op der Koordinatefliger of. Well d'Berechnungen op geschätzte Wäerter baséieren (vum virege Schrëtt), sinn de Minimum a Maximum fonnt och net ganz korrekt (awer wahrscheinlech ganz no bei de genaue Wäerter). (De Punkt (3/2, 1/16) ass ganz no beim lokalen Minimum. Vun Schrëtt 3 un, wëssen mir dat op ëmmer positiv fir NS> -1/2, a mir hunn e klenge Wäert (1/16) fonnt; also ass de Feelerwäert extrem kleng an dësem Fall.)
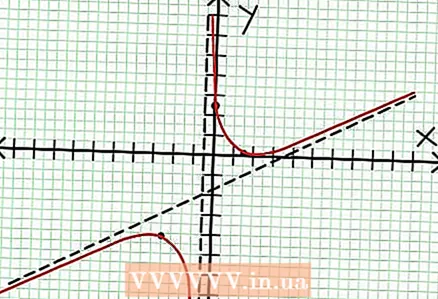8. 8 Verbënnt déi ofhängeg Punkte a verlängert d'Graf gutt mat den Asymptoten (vergiesst net iwwer déi richteg Richtung vun der Grafik déi bei den Asymptoten kënnt). Denkt drun datt d'Grafik d'X-Achs net kreest (kuckt Schrëtt 3). D'Graf schneit och net mat den horizontalen a vertikalen Asymptoten (kuckt Schrëtt 5). Ännert d'Richtung vum Diagram net ausser op den extremen Punkten, déi am virege Schrëtt fonnt goufen.

Tipps

• Wann Dir déi uewe genannte Schrëtt strikt an Uerdnung gefollegt hutt, ass et net néideg déi zweet Derivate (oder ähnlech komplex Quantitéiten) ze berechnen fir Är Léisung ze testen.
• Wann Dir d'Wäerter vun de Quantitéite net braucht ze berechnen, kënnt Dir lokal Extrema ersetzen andeems Dir e puer zousätzlech Koordinatenpaarte berechent (NS, op) tëscht all Paar Asymptoten. Ausserdeem, wann et Iech egal ass wéi déi beschriwwen Method funktionnéiert, da sidd net iwwerrascht firwat Dir d'Derivat net fanne kënnt an d'Gläichung N '(x) D (dirx) - N (dir.x) D '(dirx) = 0.
• An e puer Fäll musst Dir mat méi héije Uerdnung Polynomen schaffen. Wann Dir net déi exakt Léisung mat Faktoriséierung, Formelen, etc.
• An seltenen Fäll deelen den Teller an den Nenner e gemeinsame verännerleche Faktor. Laut de beschriwwe Schrëtt féiert dëst op Null an e vertikalen Asymptote op der selwechter Plaz. Wéi och ëmmer, dëst ass net méiglech, an d'Erklärung ass eng vun de folgenden:
  • Null an N (NS) huet eng méi héich Multiplizitéit wéi Null an D (NS). Graf F (NS) tendéiert zu Null op dësem Punkt, awer ass net do definéiert. Gitt dëst un andeems Dir e Krees ronderëm de Punkt zitt.
  • Null an N (NS) an Null an D (NS) hunn déiselwecht Villfalt. D'Grafik Approche zu engem Net-Nullpunkt bei dësem Wäert NSawer net do definéiert. Gitt dëst un andeems Dir e Krees ronderëm de Punkt zitt.
  • Null an N (NS) huet eng méi niddreg Multiplikitéit wéi Null an D (NS). Et gëtt eng vertikal Asymptote hei.